The area bounded by the curve $y = \frac{3}{| x |} and y + | 2 - x | = 2$ is

A

$\frac{π}{2}$

B

$π$

C

$2 π$

D

$3 π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$y^{2} (2 - x) = x^{2}$
$∴ y^{2} = \frac{x^{3}}{2 - x}$
$∴ y = \pm \frac{x^{3 / 2}}{\sqrt{2 - x}}, clearly x \in [0, 2]$
$Consider y = \frac{x^{3 / 2}}{\sqrt{2 - x}}$
When x=0, y=0
Also, when x increases from $' 0' to' 2', y increases from '0' \to' \infty'$
Hence graph of given relation is as shown in the following figure :

$Required Area is A = 2 \overset{2}{\int_{0}} \frac{x^{3 / 2}}{\sqrt{2 - x}} d x$
$Put x = 2 \sin^{2} θ$
$∴ A = 2 \overset{π / 2}{\int_{0}} \frac{2 \sqrt{2} \sin^{3} θ}{\sqrt{2 - 2 \sin^{2} θ}} 4 \sin θ \cos θ d θ$
$= 16 \overset{π / 2}{\int_{0}} \sin^{4} θ d θ$
$= 16 \overset{π / 2}{\int_{0}} \frac{{(1 - \cos 2 θ)}^{2}}{4} d θ$
$= 4 \overset{π / 2}{\int_{0}} (1 - 2 \cos 2 θ + \cos^{2} 2 θ) d θ$
$= 4 \overset{π / 2}{\int_{0}} (1 - 2 \cos 2 θ + \frac{1 + \cos 4 θ}{2}) d θ$
$= 4 {(θ + \sin 2 θ + \frac{θ + \frac{\sin 4 θ}{4}}{2})}_{0}^{π / 2}$
$= 4 (\frac{π}{2} + 0 + \frac{π}{4})$
$= 3 π$

|

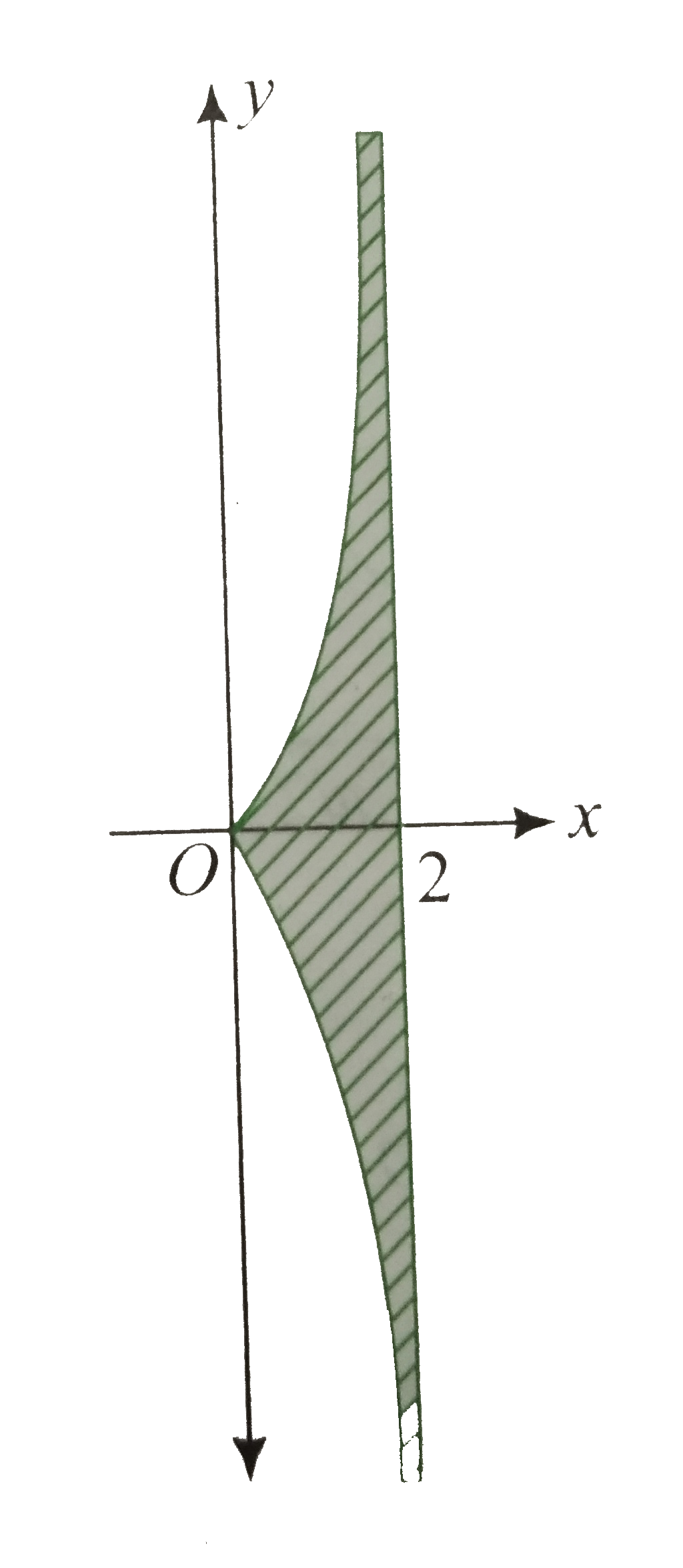
Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the curves $y = x^{2} and y = 2 - x^{2}$ is
A $\frac{8}{3}$ sq units
B $3 / 8$ sq units
C $3 \frac{/}{2}$ sq units
DNone of these
Question 2 - Select One
The area bounded by the curves $y^{2} = x^{3} and | y | = 2 x$ is
A $\frac{5}{16}$ sq units
B $\frac{16}{5}$ sq units
C $\frac{3}{8}$ sq units
DNone of these
Question 3 - Select One
The area bounded by the curves $y = - x^{2} + 2 and y = 2 | x | - x$ is
A $2 / 3$
B $8 / 3$
C $4 / 3$
DNone of these

CENGAGE-AREA-Exercise (Single)

Home
Ask Doubt
Profile