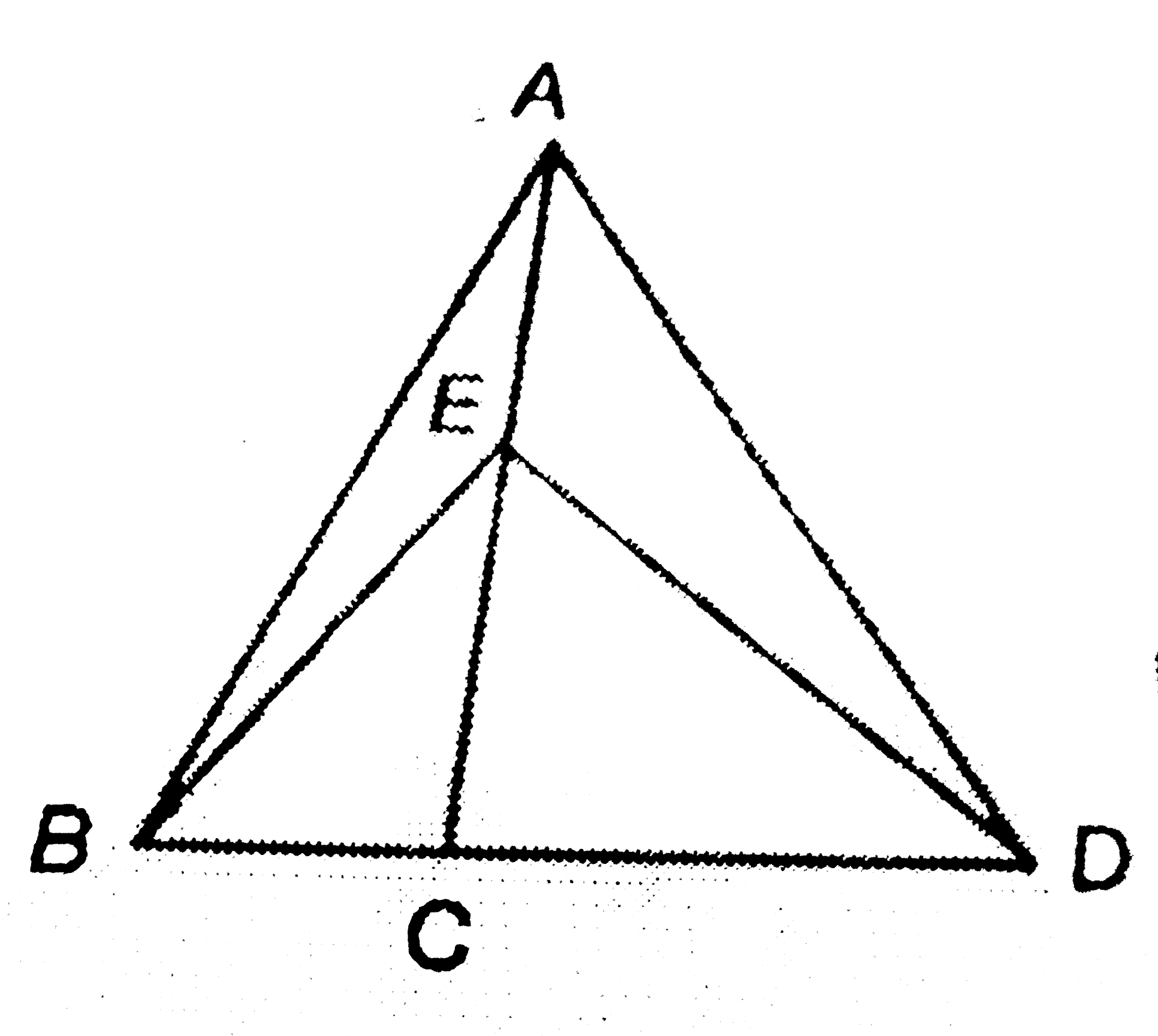
If BC:CD=2:2, AE:EC=2:3, then find the ratio of the area of the △ECD to the area of △AEB.
2:1
2:3
3:5
4:3
The correct Answer is:A
i) As BC:CD=2:3, Area (△ABC):Area(△ACD)=2:3
Let area of △ABC=2x and (△ACD)=3x.
i) As AE:EC=3:4, Area (△AEB)=37(3x) and Area(△ECD)=47(3x).
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
Knowledge Check
In the diagram AD = DB and AH = HD Find the ratio of the area of the shaded portion to that of the triangle DEF, if DE || BC and HG || AE
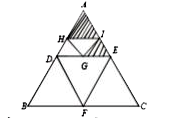 A2:3B1:3C1:2D1:113
A2:3B1:3C1:2D1:113In the figure, what is the area of ΔABC if EC|CD = 3 ?
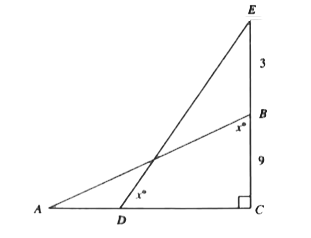 A12B24C81D121.5
A12B24C81D121.5
In a ΔABC,AD:DB=1:3,AE:EC=2:3,BF:FC=1:2. Find the ratio of area of Δ of ΔDEF:ΔABC.
View SolutionIn Fig. 9.29 ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of triangle ACD.

View SolutionIn figure, DE||BC and the ratio of the areas of △ADEand trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
View SolutionIn figure, DE||BC and the ratio of the areas of △ADEand trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
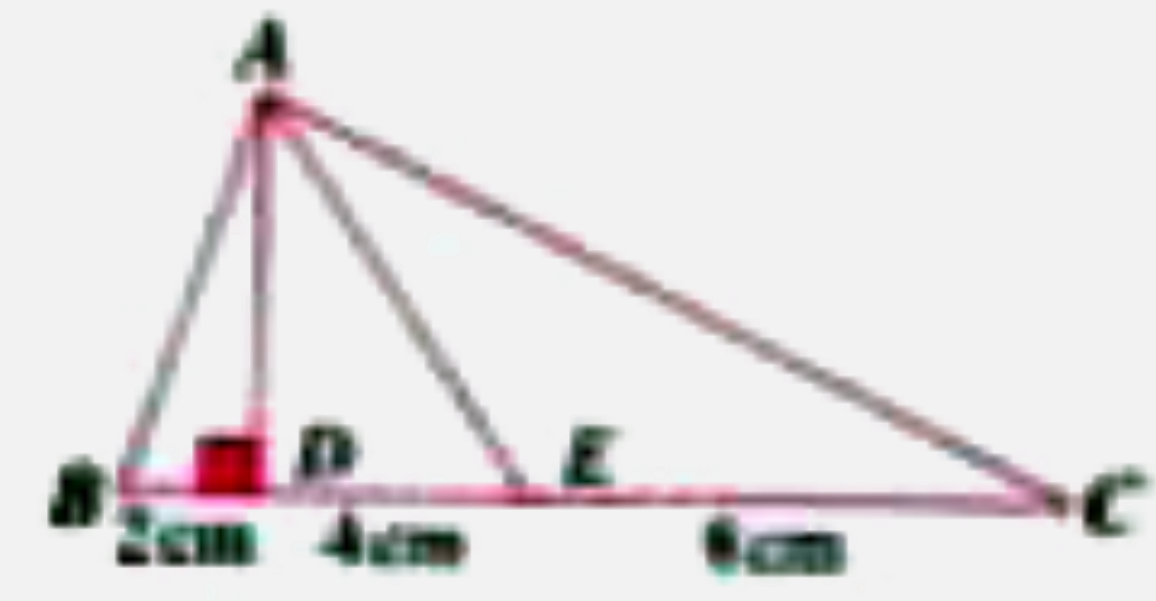
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
View SolutionIn ΔABC there are 2 points D and E on BC such that BD:DE:EC=3:4:5, if the area of ΔADE=40cm2 then find the area of ΔABC .
View Solution
