In the adjoining figure, ABC is a triangle and D is any point in its interior. Show that (BD+DC)<(AB+AC).
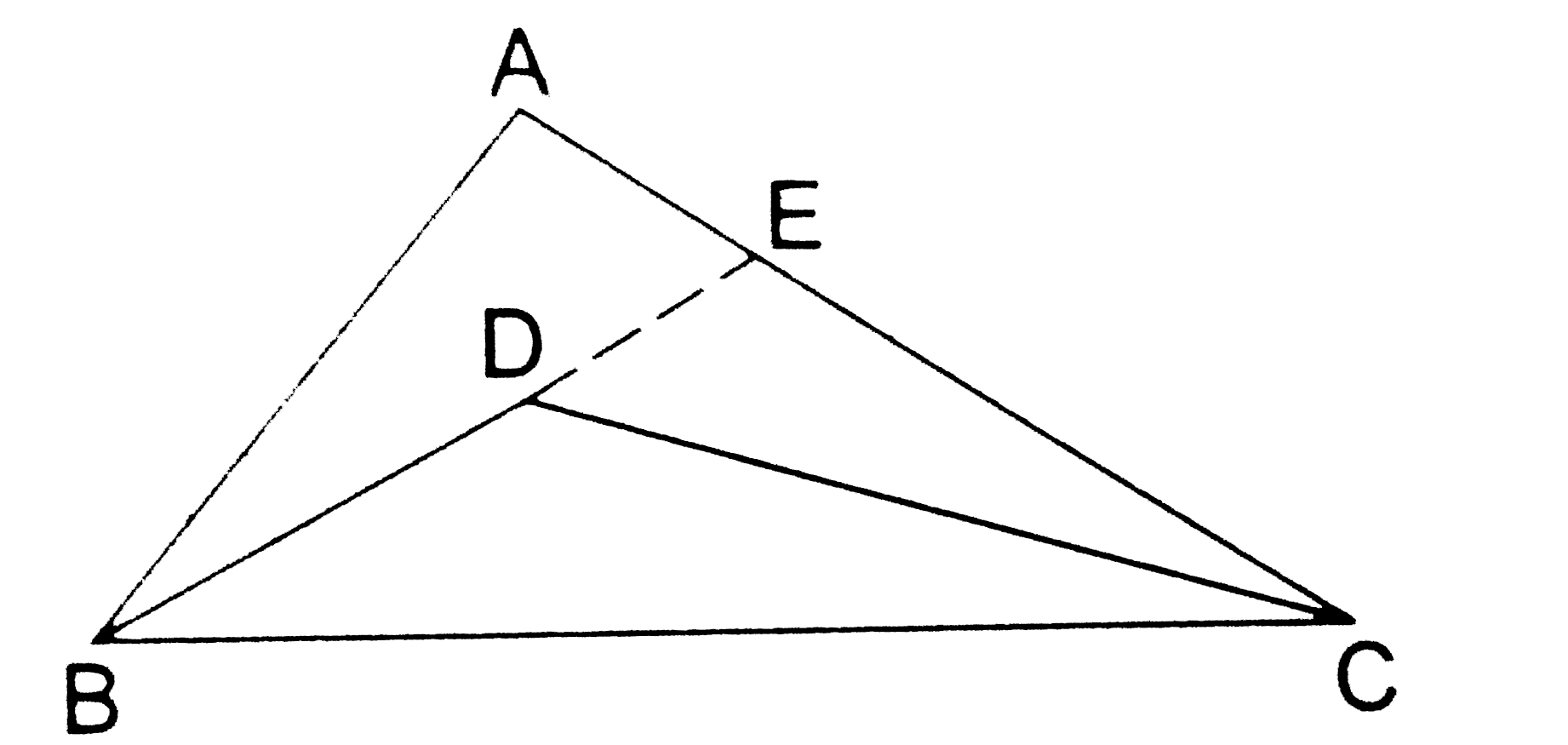
Produce BD to meet AC at E.
We know that in a triangle, the sum of any two sides is always greater than the third side.
In ΔABE, we have
AB+AE>BE⇒AB+AE>BD+DE …(i)
In ΔCDE, we have
DE+EC>DC. ...(ii)
From (i) and (ii), we get
AB+AE+DE+EC>BD+DE+DC
⇒ AB+(AE+EC)>BD+DC
⇒ (AB+AC)>(BD+DC).
Hence, (BD+DC)<(AB+AC).
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View SolutionIn the adjoinng figure, ΔABC is an isoceless triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠Aand∠D.
View SolutionIn the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionIn the adjoining figure, ABC is a triangle in whcich AB=AC. If D and E are poitns on AB and AC respecrtively such that AD=AE, show that the points B,C,E and D are concyclic.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
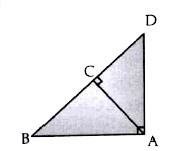
AD2=BD×DC
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that

AB2=BC×BD
View Solution
