What is the focal distance of any point $P (x_{1}, y_{1})$ on the parabola $y^{2} = 4 a x$ ?

$x_{1} + y_{1}$

$x_{1} y_{1}$

$a x_{1}$

$a + x_{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

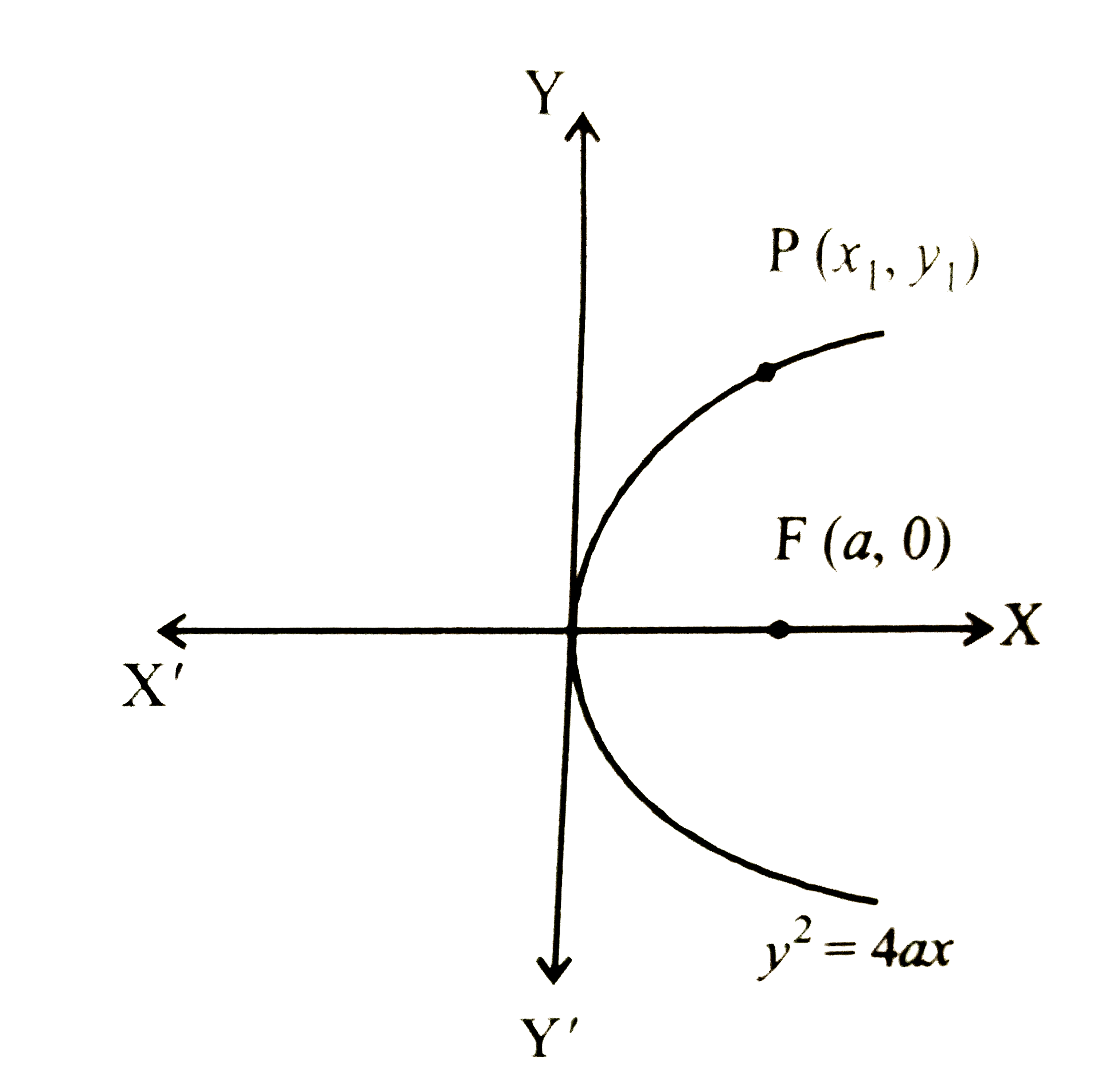
Focal distance and parameter of the point $(\frac{1}{2}, 2)$ on the parabola $y^{2} = 8 x$ are
A $\frac{2}{5}, 2$
B $5, \frac{1}{2}$
C $\frac{5}{2}, 2$
D $\frac{5}{2}, \frac{1}{2}$
If focal distance of a point P on $y^{2} = 8 x$ is 4, then P is
A $(- 2, \pm 4)$
B $(2, \pm 4)$
C $(4, \pm 2)$
D $(\pm 4, 2)$
If focal distance of point P on $y^{2} = 4 x$ is 6, then P is
A $(5, \pm 2 \sqrt{5})$
B $(5, \pm \sqrt{5}$
C $(\sqrt{5}, \pm 5)$
D $(5, 5)$