In the figure, the two triangles are congruent.The corresponding parts are marked. We can Write ΔRATE ?
To determine the congruence of triangles RAT and WON, we can follow these steps:
Step 1: Identify the Given Information
We are given that triangles RAT and WON are congruent. The corresponding parts of the triangles are marked as follows:
- AR = WO
- AT = NO
- ∠A = ∠O
- ∠R = ∠W
- ∠T = ∠N
Step 2: Write the Congruence Statement
Since the triangles are congruent, we can write the congruence statement as:
ΔRAT ≅ ΔWON
Step 3: Justify the Congruence
To justify the congruence of the triangles, we can use the Angle-Side-Angle (ASA) and Side-Angle-Side (SAS) congruence rules:
- ASA Rule: We have two angles (∠A and ∠R) and the included side (AR) that are equal in both triangles.
- SAS Rule: We can also consider two sides (AR and AT) and the included angle (∠R) to show that the triangles are congruent.
Conclusion
Based on the information provided and the congruence rules applied, we conclude that:
ΔRAT ≅ ΔWON
---
We are given that triangles RAT and WON are congruent. The corresponding parts of the triangles are marked as follows:
- AR = WO
- AT = NO
- ∠A = ∠O
- ∠R = ∠W
- ∠T = ∠N
Since the triangles are congruent, we can write the congruence statement as:
ΔRAT ≅ ΔWON
To justify the congruence of the triangles, we can use the Angle-Side-Angle (ASA) and Side-Angle-Side (SAS) congruence rules:
- ASA Rule: We have two angles (∠A and ∠R) and the included side (AR) that are equal in both triangles.
- SAS Rule: We can also consider two sides (AR and AT) and the included angle (∠R) to show that the triangles are congruent.
Based on the information provided and the congruence rules applied, we conclude that:
ΔRAT ≅ ΔWON
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBOOK - NCERT ENGLISHCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - EXERCISE 7.1
4 Videos
- CONGRUENCE OF TRIANGLESBOOK - NCERT ENGLISHCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - SOLVED EXAMPLES
9 Videos
- COMPARING QUANTITIESBOOK - NCERT ENGLISHCHAPTER - COMPARING QUANTITIESEXERCISE - EXERCISE 8.2
10 Videos
- DATA HANDLINGBOOK - NCERT ENGLISHCHAPTER - DATA HANDLINGEXERCISE - EXERCISE 3.2
5 Videos
Similar Questions
Knowledge Check
While working on a gerometry problem Raul determines that the angles of one triangle are congruent to the corresponding angles of another triangle. Which of the following is valid deduction that Raul can make?
AThe two triangles are congruent but not necessarily similar.BThe two triangles are similar but not necessarily congruent.CThe two triangles are both similar and congruent.DThe two triangle are neither similar nor congruent.
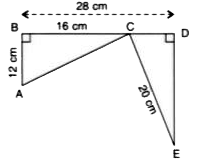
Show that the two triangles given the following figure are congruent.
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600 If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionTwo triangles are congruent if include two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. GIVE : Two △ABC and DEF such that ∠B=∠E,∠C=∠F and BC=EF TO PROVE : △ABC≅△DEF
View SolutionTheorem 6.4 : If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similiar
View SolutionGiven below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form. ΔDEF
View SolutionGiven below are measurements of some parts of two triangles. Examinewhether the two triangles are congruent or not, using RHS congruencerule. In case of congruent triangles, write the result in symbolic form
View SolutionWhich of the following pairs of triangle are congruent by ASA condition?
View Solution
