Fig., shows the stress-strain curve for a given materal. What are (a) Young's modulus and (b) approximate yield strength for this material?
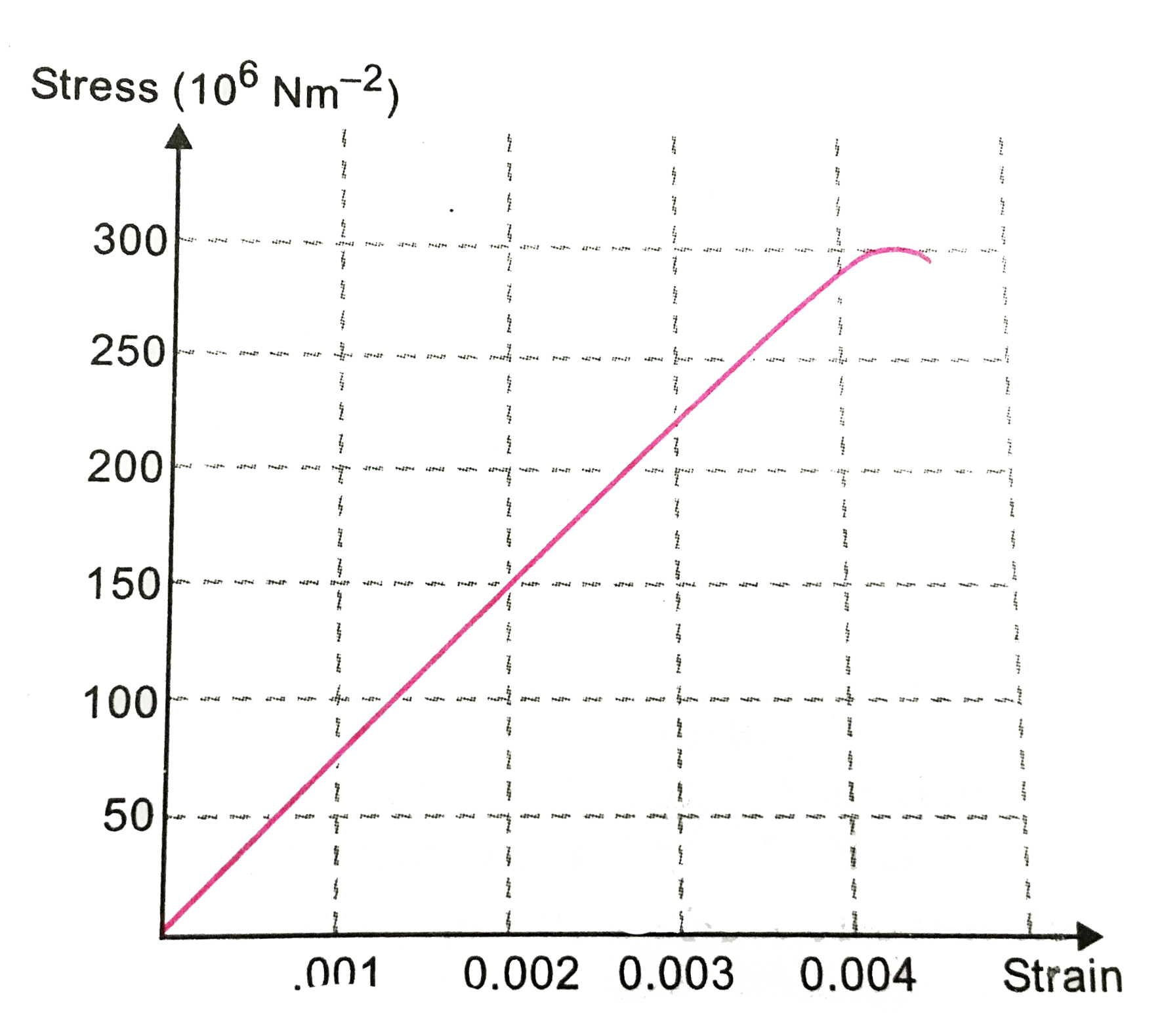
It is clear from the given graph that for stress 150 ×106N/m2 , strain is 0.002.
∴ Young's modulus, Y = StressStrain
=150×1060.002=7.5×1010N/m2
Hence, Young’s modulus for the given material is 7.5 ×1010N/m2.
(b) The yield strength of a material is the maximum stress that the material can sustain without crossing the elastic limit.
It is clear from the given graph that the approximate yield strength of this material is
300×106N/m2or3×108N/m2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- MOTION IN A PLANE BOOK - NCERT ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE
32 Videos
Similar Questions
Knowledge Check
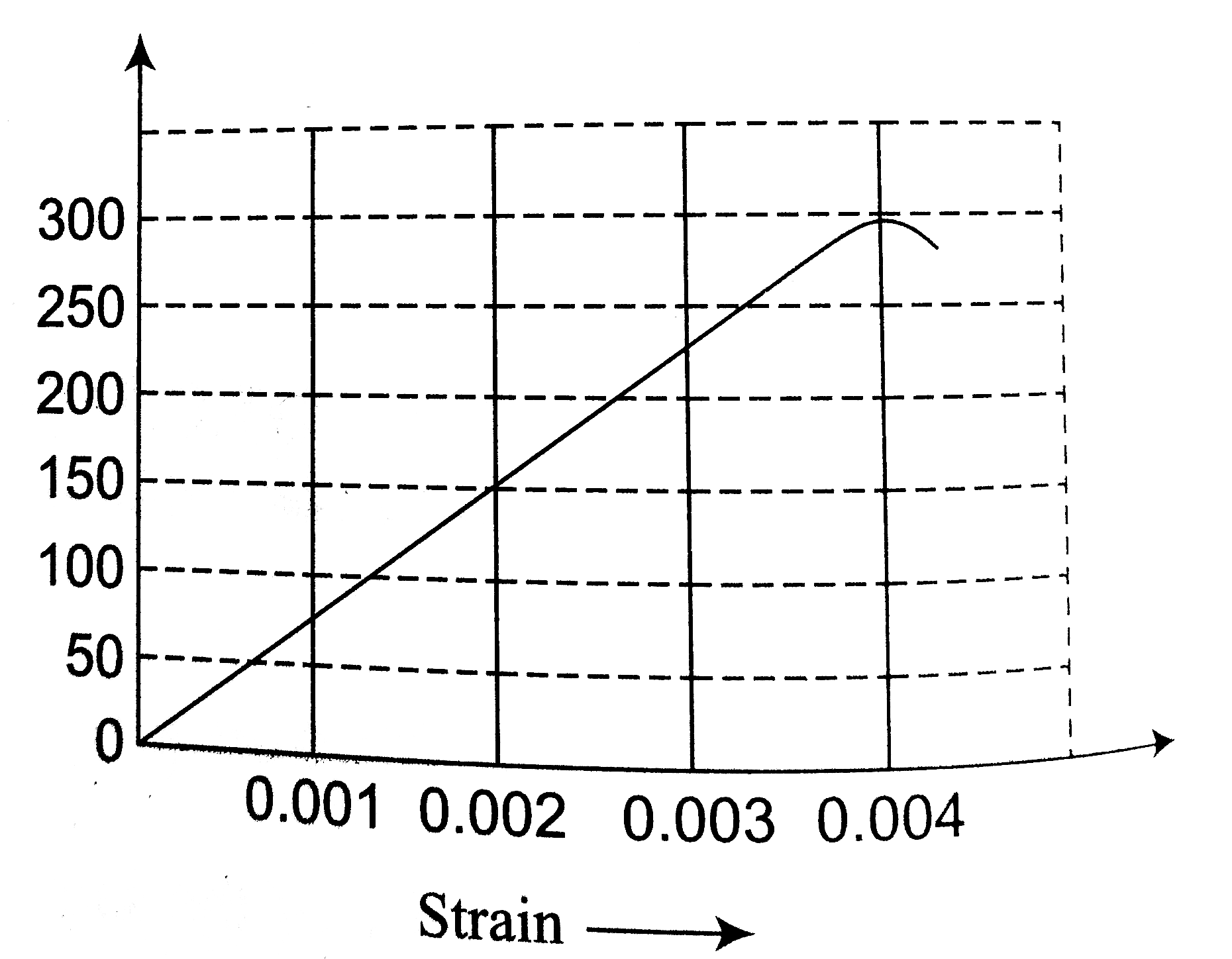
Figure shows the strain stress curve for a given material. The Young's modulus of the material isA5×109Nm−2B5×1010Nm−2C7.5×109Nm−2D7.5×1010Nm−2
Stress-strain curve for four metals are shown in figure. The maximum Young's modulus of elasticity is for metal

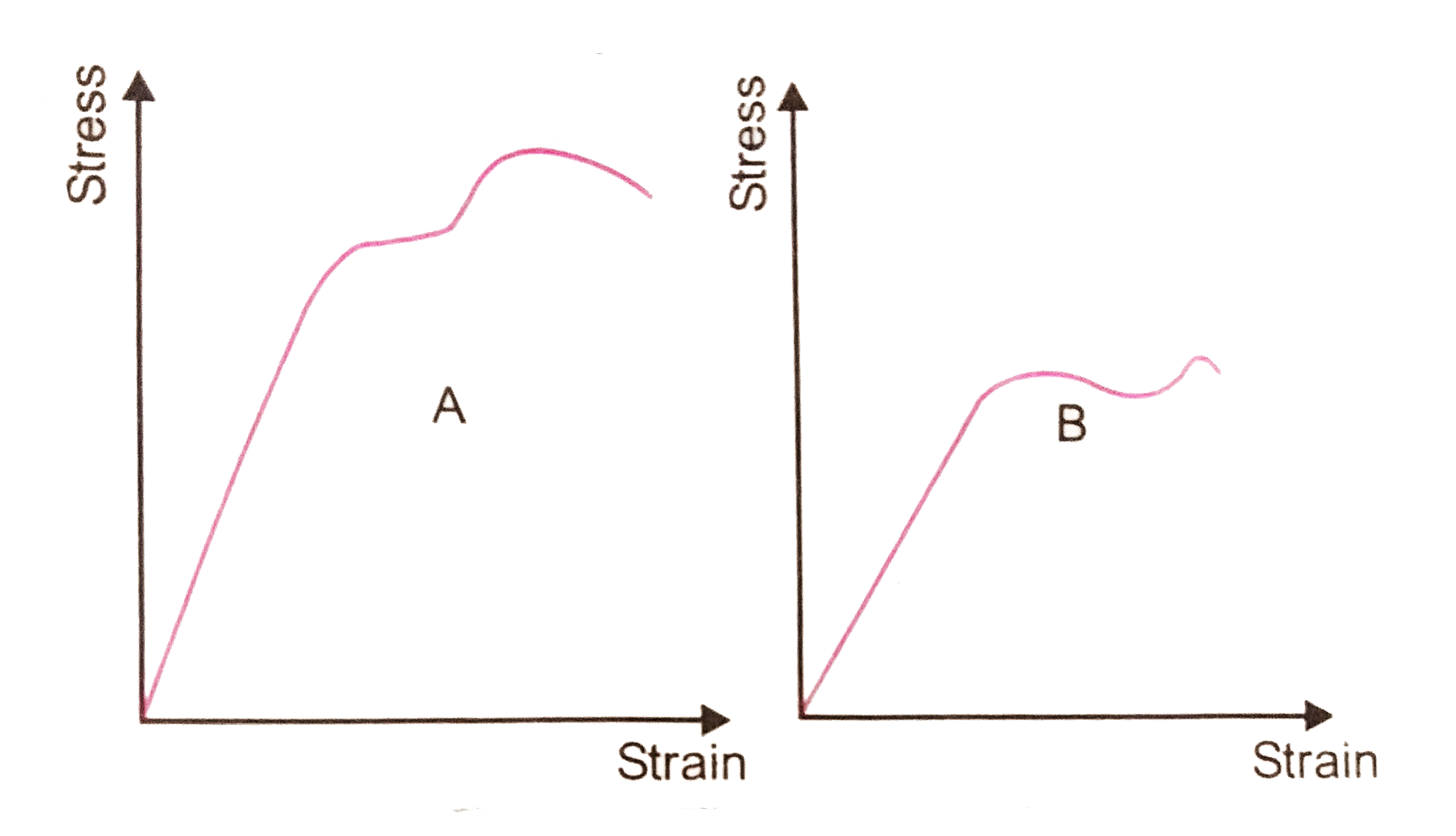
View SolutionThe stress versus strain graph for two materials A and B are shown in fig. the graph are on the same scale. ltbr> (a) Which material has greater Young's modulus?
(b) which of the two is stronger material?
View SolutionThe stress-strain graphs for two materials A and B are shown in the figure. The graphs are drawn to the same scale.
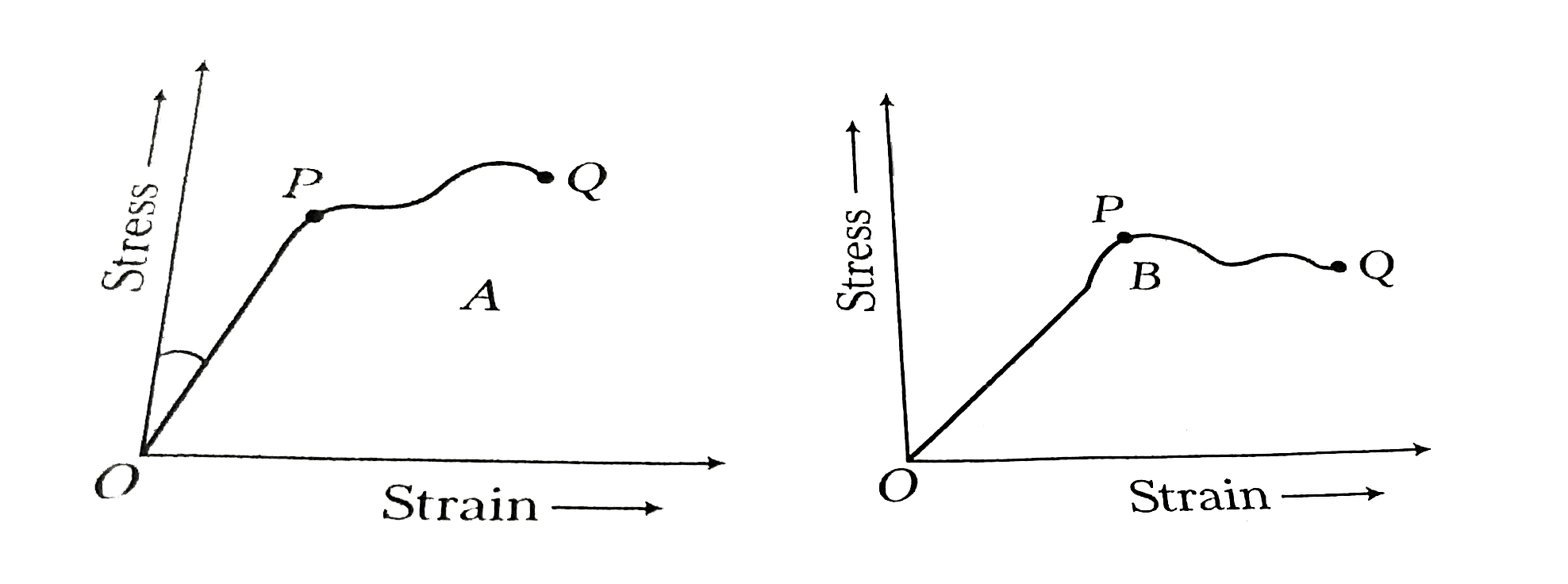
(a) Which material has a greater Young's modulus ?
(b) Which material is more ductile ?
(c) Which material is more brittle?
(d) Which of the two is the stronger material ?
View SolutionFigure shows the stress-strain curve of two metals P and Q . From the graph, it can be concluded that

View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View Solution

