A mild steel wire of length 1.0 m and cross-sectional are 0.5×10−20cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=2×1011Nm−2.
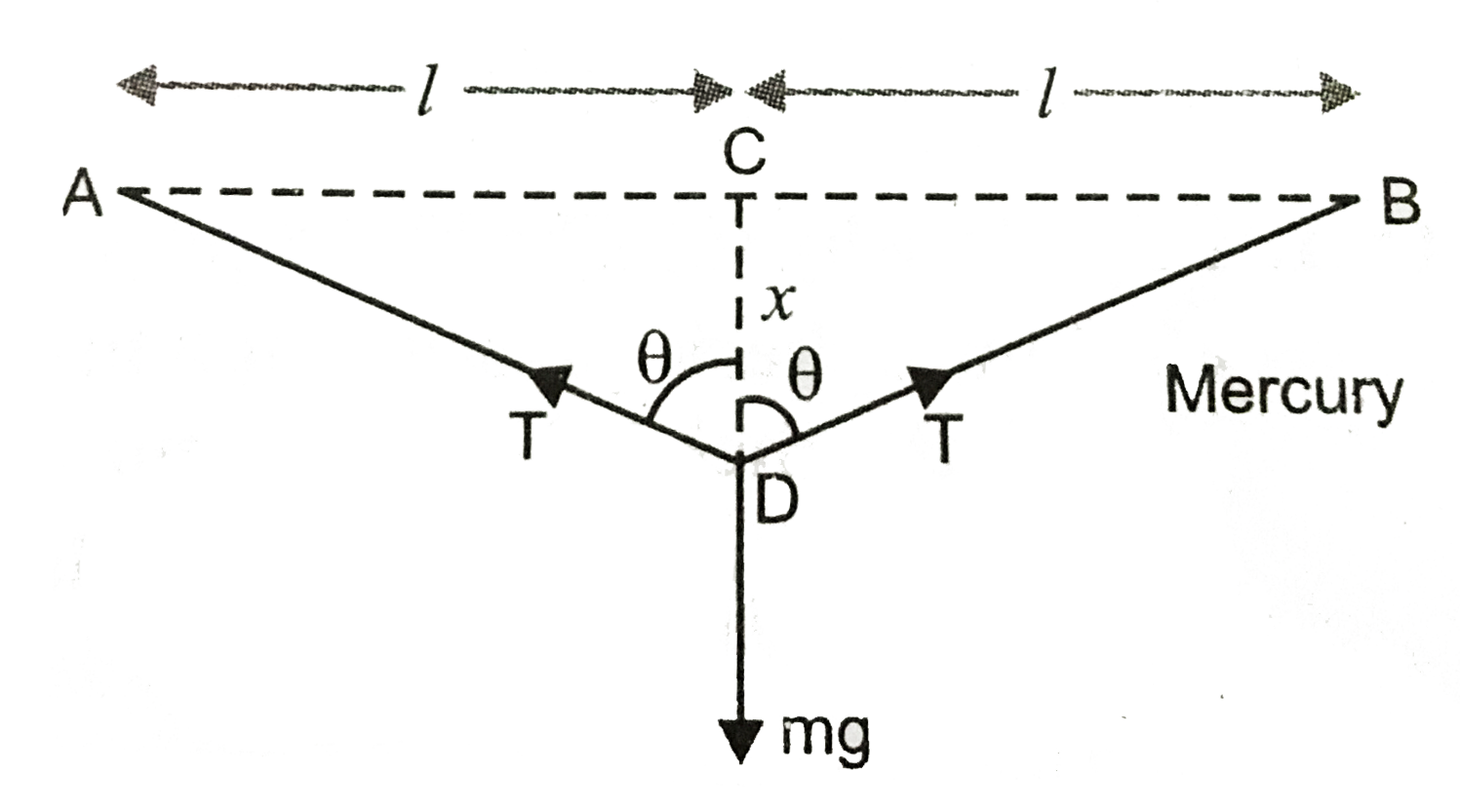
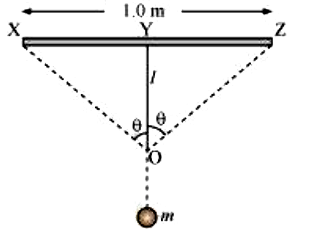
Length of the steel wire = 1.0 m
Area of cross-section, A = 0.50 ×10−2cm2=0.50×10−6m2
A mass 100 g is suspended from its midpoint.
m = 100 g = 0.1 kg
Hence, the wire dips, as shown in the given figure.
Original length = XZ
Depression = l
The length after mass m, is attached to the wire = XO + OZ
Increase in the length of the wire:
Δl=(XO+OZ)−XZ
Where, XO=OZ=[(0.5)2+l2]12
∴Δl=2[(0.5)2+(l)2]12−1.0
2×0.5[1+(l0.5)2]12−1.0
Expanding and neglecting higher terms, we get:
Δl=l20.5
Strain = Increase in lengthOriginal length
Let T be the tension in the wire.
∴mg=2Tcosθ
Using the figure, it can be written as:
cosθ=l((0.5)2+l2)12
=l(0.5)(1+(l0.5)2)12
Expanding the expression and eliminating the higher terms:
cosθ=l(0.5)(1+l22(0.5)2)
(1+l20.5)≅1 for small l
∴cosθ=l0.5
∴T=mg2(l0.5)=mg×0.52l=mg4l
Stress = TensionArea=mg4l×A
Young's modulus = =StressStrain
Y=mg×0.54l×A×l2
l=3√mg×0.54YA
Young’s modulus of steel, Y= 2×1011 Pa
∴l=√0.1×9.8×0.54×2×1011×0.50×10−6
= 0.0106 m
Hence, the depression at the midpoint is 0.0106 m.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- MOTION IN A PLANE BOOK - NCERT ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE
32 Videos
Similar Questions
A mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
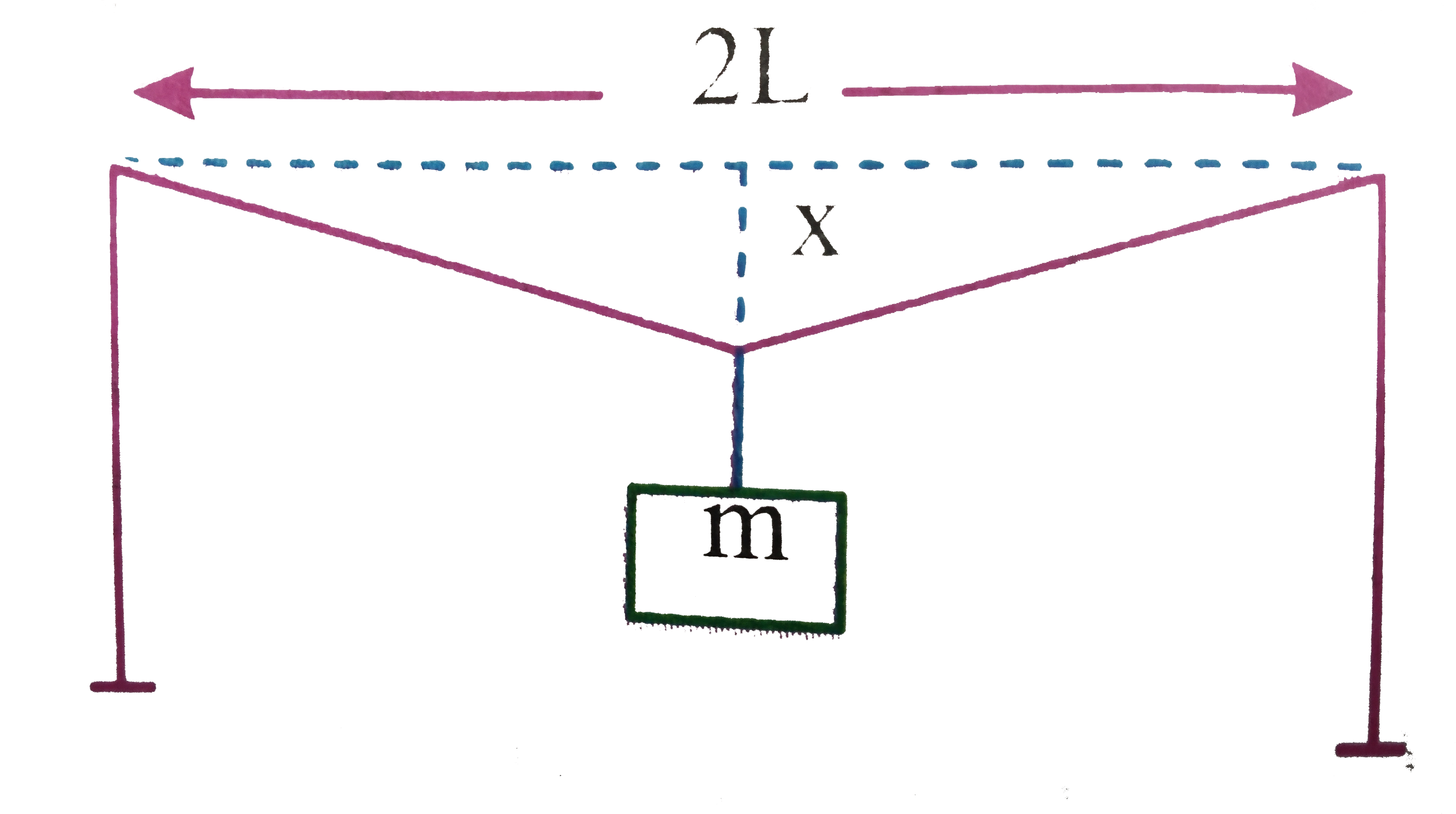
View Solution
Knowledge Check
A mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
 Ax22L2BxLCx2/LDx2/2L
Ax22L2BxLCx2/LDx2/2LA mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
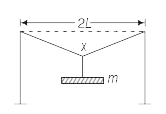 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22LA mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
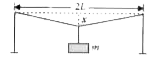
A mass m is suspended from the midpoint of the wire. Strain in the wire isAx22L2BxLCx2LDx22L
A steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to
View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is X. Strain in the wire is proportional to
View SolutionA steel wire of original length 1m and cross-sectional area 4.00mm2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16kg is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel =2.0×1011Nm−2. Take g=10ms−2
View SolutionA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
View SolutionA mild steel wire of length 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is

View Solution
