A rigid bar of mass 15 kg is supported symmetrically by three wires each 2 m long. Those at each end are of copper and middle one is of iron. Determine the ratio of their diameters if each is to have the same tension. Young's modulus of elasticity for copper and steel are 110×109Nm−2 and 190×109Nm−2 respectively.
To solve the problem of determining the ratio of the diameters of the wires made of copper and iron that support a rigid bar symmetrically, we can follow these steps:
Step 1: Understand the Problem
We have a rigid bar of mass 15 kg supported by three wires (two copper and one iron). Each wire has the same length of 2 m, and we need to find the ratio of their diameters when the tension in each wire is the same.
Step 2: Identify Given Data
- Mass of the rigid bar, m=15kg
- Length of each wire, L=2m
- Young's modulus for copper, Yc=110×109N/m2
- Young's modulus for iron, Yi=190×109N/m2
Step 3: Establish the Relationship
Young's modulus Y is defined as:
Y=StressStrain=F/AΔL/L
Where:
- F is the force (tension in the wire),
- A is the cross-sectional area of the wire,
- ΔL is the change in length,
- L is the original length.
Since the tension in each wire is the same and the strain is constant, we can express the area A in terms of diameter d:
A=πd24
Step 4: Relate Young's Modulus to Diameter
From the definition of Young's modulus, we can rearrange it to find the relationship between Young's modulus and diameter:
Y∝FA⋅Strain⇒Y∝F⋅LΔL⋅πd24
Since F and L are constants, we can simplify this to:
Y∝1d2
Step 5: Set Up the Ratio of Diameters
From the relationship above, we can write:
d2cd2i=YiYc
Where:
- dc is the diameter of the copper wire,
- di is the diameter of the iron wire.
Taking the square root gives:
dcdi=√YiYc
Step 6: Substitute the Values
Now, substituting the values of Young's modulus:
dcdi=√190×109110×109=√190110=√1.7272≈1.31
Step 7: Final Ratio
Thus, the ratio of the diameters of the copper wire to the iron wire is:
dcdi≈1.31:1
Conclusion
The final answer is that the ratio of the diameters of the copper wire to the iron wire is approximately 1.31:1.
---
We have a rigid bar of mass 15 kg supported by three wires (two copper and one iron). Each wire has the same length of 2 m, and we need to find the ratio of their diameters when the tension in each wire is the same.
- Mass of the rigid bar, m=15kg
- Length of each wire, L=2m
- Young's modulus for copper, Yc=110×109N/m2
- Young's modulus for iron, Yi=190×109N/m2
Young's modulus Y is defined as:
Y=StressStrain=F/AΔL/L
Where:
- F is the force (tension in the wire),
- A is the cross-sectional area of the wire,
- ΔL is the change in length,
- L is the original length.
A=πd24
From the definition of Young's modulus, we can rearrange it to find the relationship between Young's modulus and diameter:
Y∝FA⋅Strain⇒Y∝F⋅LΔL⋅πd24
Since F and L are constants, we can simplify this to:
Y∝1d2
From the relationship above, we can write:
d2cd2i=YiYc
Where:
- dc is the diameter of the copper wire,
- di is the diameter of the iron wire.
dcdi=√YiYc
Now, substituting the values of Young's modulus:
dcdi=√190×109110×109=√190110=√1.7272≈1.31
Thus, the ratio of the diameters of the copper wire to the iron wire is:
dcdi≈1.31:1
The final answer is that the ratio of the diameters of the copper wire to the iron wire is approximately 1.31:1.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:EXERCISE
Explore 21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EXERCISE
Explore 31 Videos
- MOTION IN A PLANE Book:NCERT ENGLISHChapter:MOTION IN A PLANE Exercise:EXERCISE
Explore 32 Videos
Similar Questions
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
View Solution
Knowledge Check
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
AYcopperYironB√YcopperYironCY2ironY2copperDYironYcopper
A rigid bar of mass 15 kg is supported symmetrically by three wires, each of length 2 m. The wires at the endpoints are made of copper and the middle one is made of steel. If the tension in each wire is the same, then the diameter of copper wire to the diameter of steel wire is [Given, Ycopper=1.1×1011N m−1andYsteel=1.9×1011N m−2]
View SolutionA sonometer wire of length 1.5m is made of steel. The tension in it produces an elastic strain of 1%. What is the fundamental frequency of steel if density and elasticity of steel are 7.7×103kg/m3 and 2.2×1011N/m2 respectively ?
View SolutionHow much should the pressure on a litre of water be changed to compress it by 0.10%? Bulk modulus of elasticity of water = 2.2×109Nm−2.
View SolutionA block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
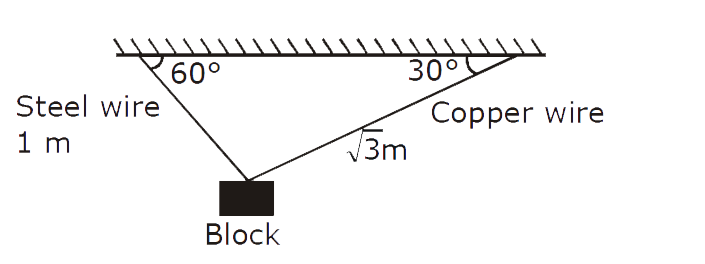
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]
View SolutionCalculate the Poisson's ratio for steel. Given that Young's modulus is 2×1011Nm−2 and rigidity modulus is 8×1010Nm−2.
View SolutionFor steel the Young modulus of elasticity is 2.9×1011Nm−2 and density is 8×103kgm−3. Find the velocity of the longitudinal waves in steel.
View SolutionA steel wire of length 600cm and diameter 1.2 mm is stretched through 4 mm by a load. Calculate the work done. Young's modulus of steel =2×1011Nm−2.
View Solution