A 70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m rotating about its vertical axis. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
To solve the problem, we need to determine the minimum rotational speed (angular velocity, ω) of a hollow cylindrical drum that allows a 70 kg man to remain stuck against the wall when the floor is suddenly removed.
1. Identify Forces Acting on the Man:
- The weight of the man (W) acts downward:
W=mg
where m=70kg and g=9.8m/s2.
- The normal force (N) acts horizontally towards the center of the cylinder.
- The frictional force (F) acts upward, opposing the weight of the man.
2. Set Up the Equations:
- The frictional force can be expressed as:
F=μN
where μ=0.15 is the coefficient of friction.
- The centripetal force required to keep the man moving in a circle is provided by the normal force:
N=mv2r
where r=3m is the radius of the cylinder and v is the tangential speed.
3. Relate Tangential Speed to Angular Velocity:
- The relationship between tangential speed v and angular velocity ω is given by:
v=rω
- Substituting this into the centripetal force equation gives:
N=m(rω)2r=mrω2
4. Equate Forces for the Man to Stay Stuck:
- For the man to remain stuck against the wall, the frictional force must equal the weight:
F=mg
- Substituting the expression for frictional force:
μN=mg
- Now substituting N:
μ(mrω2)=mg
5. Solve for Angular Velocity ω:
- Cancel m from both sides:
μrω2=g
- Rearranging gives:
ω2=gμr
- Taking the square root:
ω=√gμr
6. Substitute the Values:
- Plug in g=9.8m/s2, μ=0.15, and r=3m:
ω=√9.80.15×3=√9.80.45=√21.78≈4.66rad/s
Final Answer:
The minimum rotational speed of the cylinder is approximately 4.66rad/s.
- The weight of the man (W) acts downward:
W=mg
where m=70kg and g=9.8m/s2.
- The normal force (N) acts horizontally towards the center of the cylinder.
- The frictional force (F) acts upward, opposing the weight of the man.
- The frictional force can be expressed as:
F=μN
where μ=0.15 is the coefficient of friction.
- The centripetal force required to keep the man moving in a circle is provided by the normal force:
N=mv2r
where r=3m is the radius of the cylinder and v is the tangential speed.
- The relationship between tangential speed v and angular velocity ω is given by:
v=rω
- Substituting this into the centripetal force equation gives:
N=m(rω)2r=mrω2
- For the man to remain stuck against the wall, the frictional force must equal the weight:
F=mg
- Substituting the expression for frictional force:
μN=mg
- Now substituting N:
μ(mrω2)=mg
- Cancel m from both sides:
μrω2=g
- Rearranging gives:
ω2=gμr
- Taking the square root:
ω=√gμr
- Plug in g=9.8m/s2, μ=0.15, and r=3m:
ω=√9.80.15×3=√9.80.45=√21.78≈4.66rad/s
The minimum rotational speed of the cylinder is approximately 4.66rad/s.
Topper's Solved these Questions
Similar Questions
A 70kg man stands in contact against the inner wall of a hollw cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing nis 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View SolutionA 70 kg man stands in contact against the wall of a cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15 m What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View SolutionA block of mass 10 kg in contact against the inner wall of a hollow cylindrical drum of radius 1m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
View SolutionA 70 kg man standing on ice throws a 3 kg body horizontally at 8m//s. The friction coefficient between the ice and his feet is 0.02. The distance, the man slip is
View SolutionA block is mass m moves on as horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v write a. the normal force by the wall on the block. b. the frictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration (dvdt=vdvds) to obtain the speed of the block after one revoluton.
View SolutionA small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
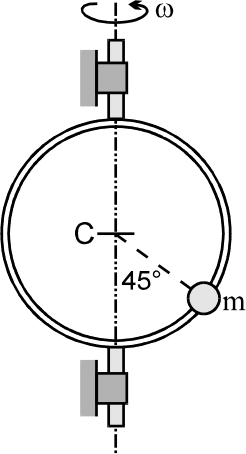 View Solution
View SolutionTwo bodies A and B of masses 5 kg and 10 kg in contact with each other rest on a table against a rigid wall as shown in fig. The coefficient of friction between the bodies and the table is 0.15. A force 200 N is applied horizontally to A. What are
(a) the reaction of the partition
(b) the action-reaction forces between A and B ?
(c) What happens when the wall is removed? Does the answer to (b) change, when the bodies are in motion? Ignore the difference between μs and μk
 View Solution
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
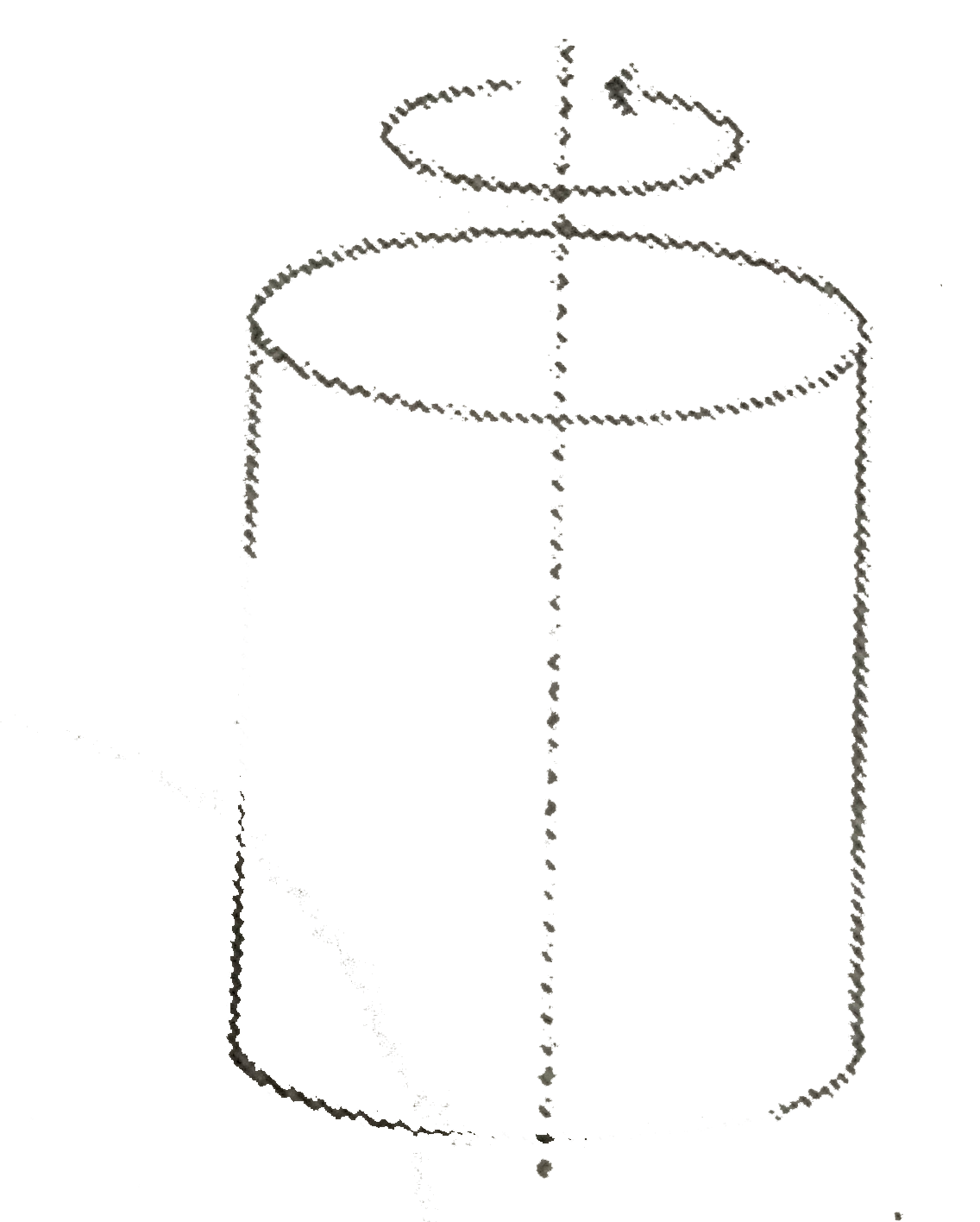 View Solution
View Solution

