If in Fig. 12.12, R1=10Ω,R2=40Ω,R3=30Ω,R5=60Ω, and a 12 V battery is connected to the arrangemtn. Calculate (a) the total resistance in the circuit, and (b) the total current flowing in the circuit.
To solve the problem step by step, we will calculate the total resistance in the circuit and then use that to find the total current flowing through the circuit.
Given:
- R1=10Ω
- R2=40Ω
- R3=30Ω
- R4=20Ω
- R5=60Ω
- Voltage of the battery V=12V
Step 1: Calculate the equivalent resistance of R1 and R2 in parallel.
The formula for the equivalent resistance R′ of two resistors in parallel is given by:
1R′=1R1+1R2
Substituting the values:
1R′=110+140
Finding a common denominator (which is 40):
1R′=440+140=540
Thus,
R′=405=8Ω
Step 2: Calculate the equivalent resistance of R3, R4, and R5 in parallel.
Using the same formula for three resistors in parallel:
1R′′=1R3+1R4+1R5
Substituting the values:
1R′′=130+120+160
Finding a common denominator (which is 60):
1R′′=260+360+160=660
Thus,
R′′=606=10Ω
Step 3: Calculate the total equivalent resistance of the circuit.
Now, R′ and R′′ are in series, so the total equivalent resistance Req is given by:
Req=R′+R′′
Substituting the values:
Req=8Ω+10Ω=18Ω
Step 4: Calculate the total current flowing in the circuit.
Using Ohm's Law, where V=I⋅R:
I=VReq
Substituting the values:
I=12V18Ω=23A
Final Answers:
(a) Total resistance in the circuit: 18Ω
(b) Total current flowing in the circuit: 23A
---
- R1=10Ω
- R2=40Ω
- R3=30Ω
- R4=20Ω
- R5=60Ω
- Voltage of the battery V=12V
(a) Total resistance in the circuit: 18Ω
Topper's Solved these Questions
Similar Questions
In the circuit, the current flowing through 10Ω resistance is
View SolutionIn the circuit diagram given below, three resistors R1,R2, and R3 of 5Ω,10Ω and 30Ω, respectively are connected as shown.

Calculate:
(a) current through each resistor.
(b) total current in the circuit.
(c) total resistance in the circuit.
View SolutionAn electric lamp, whose resistance is 20Ω and a conductor of 4Ω resistance are connected to a 6V battery as shown in (Fig. 3.18) Calculate.
(a) the total resistance of the circuit,
(b) the current through the circuit, and
( c) the potential difference across the electric lamp and the conductor.
 .
.
View Solution(a) Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) If R1=10Ω,R2=20ΩandR3=30Ω, calculate the effective resistance when they are connected in series to a battery of 6 V. Also find the current flowing in the circuit.
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View SolutionIn the given circuit, R1 = 10Ω R2=6Ω and E = 10V, then correct statement is
View SolutionIn the given circuit, calculate -

(a) the total resistance of the circuit,
(b) the current through the circuit, and
(c) the potential differences across R1andR2
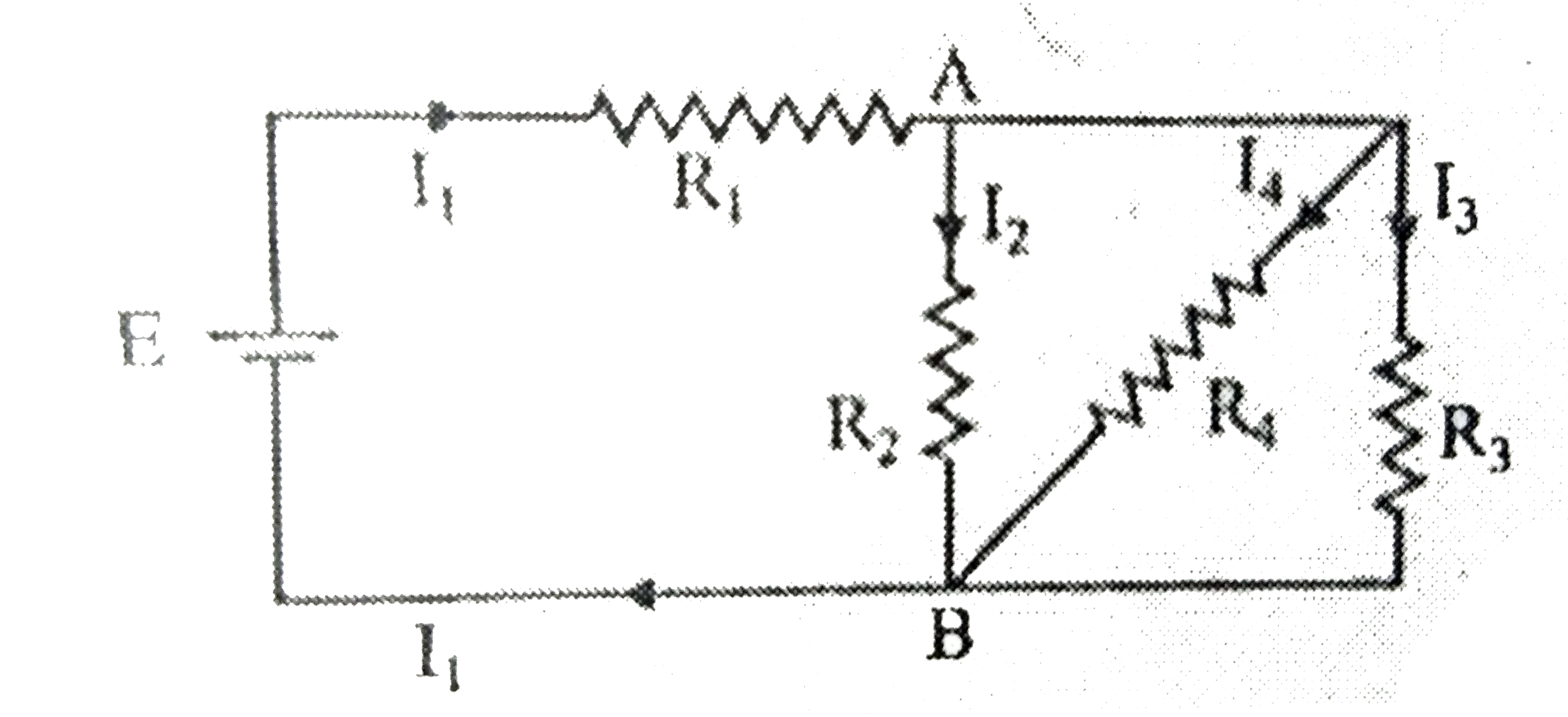
View SolutionIn the circuit shown, R1=4Ω,R2=R3=15Ω,R4=30ΩandE=10V. Caculate the equivalent resistance of te circuit and the current in each resistor.
View SolutionIn the circuit shown in fig. R1=10Ω,R2=5Ω,C1=1μF,C2=2μF, and E =6V. Calculate the charge on each capactor in the stedy state.

View SolutionIn the circuit shown, R1=2Ω,R2=R3=10Ω,R4=20ΩandE=6V. Work out the equivalent resistance of the circuit and the current in each resistor.
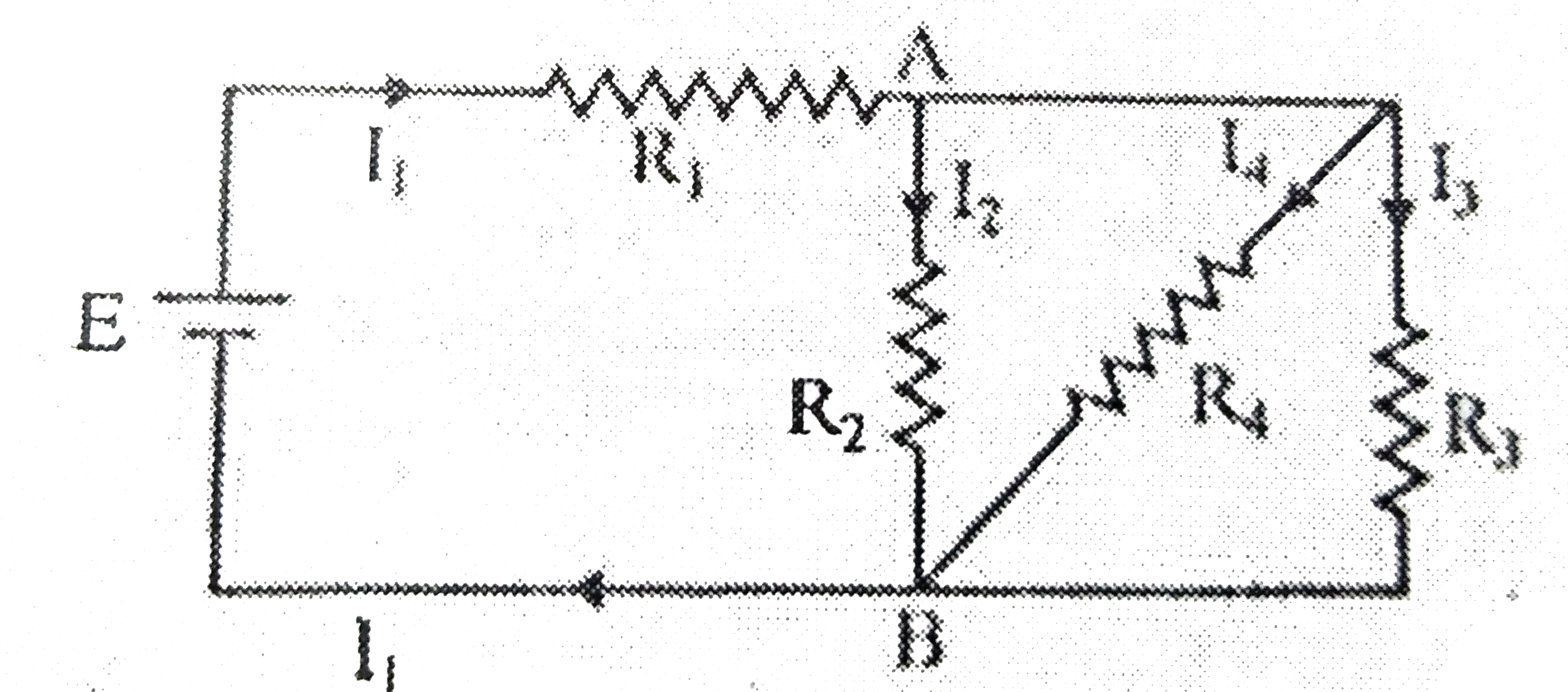
View Solution