Judge the equivalent resistance when the following are connected in parallel.
(a) 1Ωand106Ω
(b) 1Ωand103Ωand106Ω.
(a) When 1Ωand 106Ω are connected in parallel :
Let R be the equivalent resistance.

Therefore, equivalent resistance ≈1Ω
(b) When 1Ωand 106Ω are connected in parallel:
Let R be the equivalent resistance.

Therefore, equivalent resistance =0.999Ω
Topper's Solved these Questions
Similar Questions
Judge the equivalent resistance when the following are connected in parallel.
(a) 1Ωand106Ω
(b) 1Ωand103Ωand106Ω.
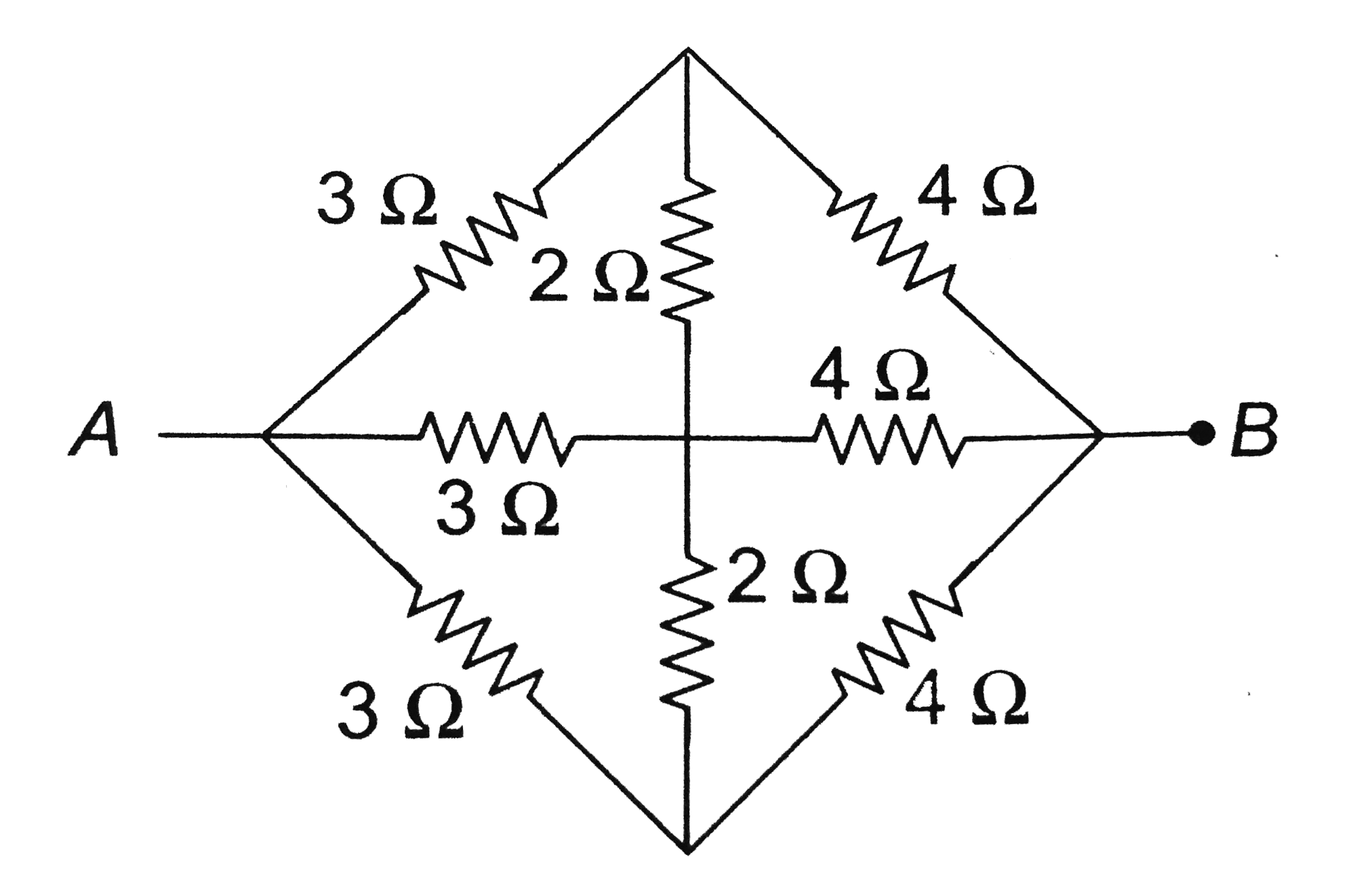
View SolutionThe equivalent resistance between A and B will be (in Ω)
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View SolutionThe equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
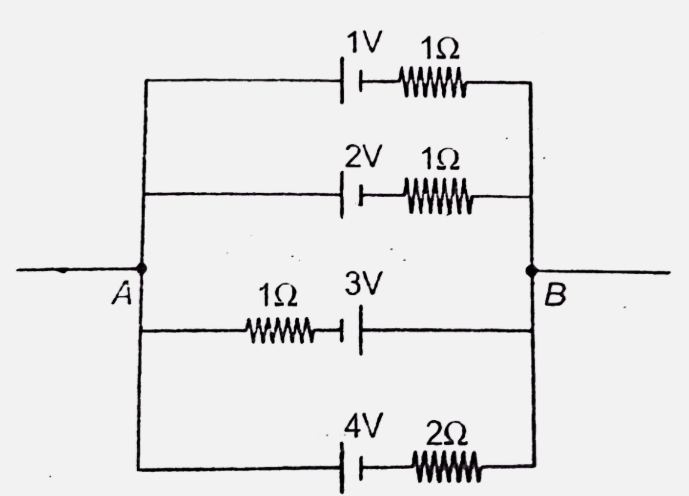
View SolutionFind equivalent emf of four different cells which are connected in parallel. Their emf's and internal resistance are 1 volt, 1Ω,2 volt, 1Ω,3 volt, 1Ω,4 volt, 2Ω and their connection is given below .
View Solution(a) Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) If R1=10Ω,R2=20ΩandR3=30Ω, calculate the effective resistance when they are connected in series to a battery of 6 V. Also find the current flowing in the circuit.
View SolutionCurrent through resistor R3 as shown in figure is ______. Given that R1=10Ω R2=5Ω R4=20Ω and R5=10Ω

View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
View SolutionThree cells of emf 3V, 4V, and 6V are connected in parallel, If their internal resistances are 1Ω, 2 Omegaand1Ω find the εeff,reff, and the current in the external load R = 1.6 Ω .
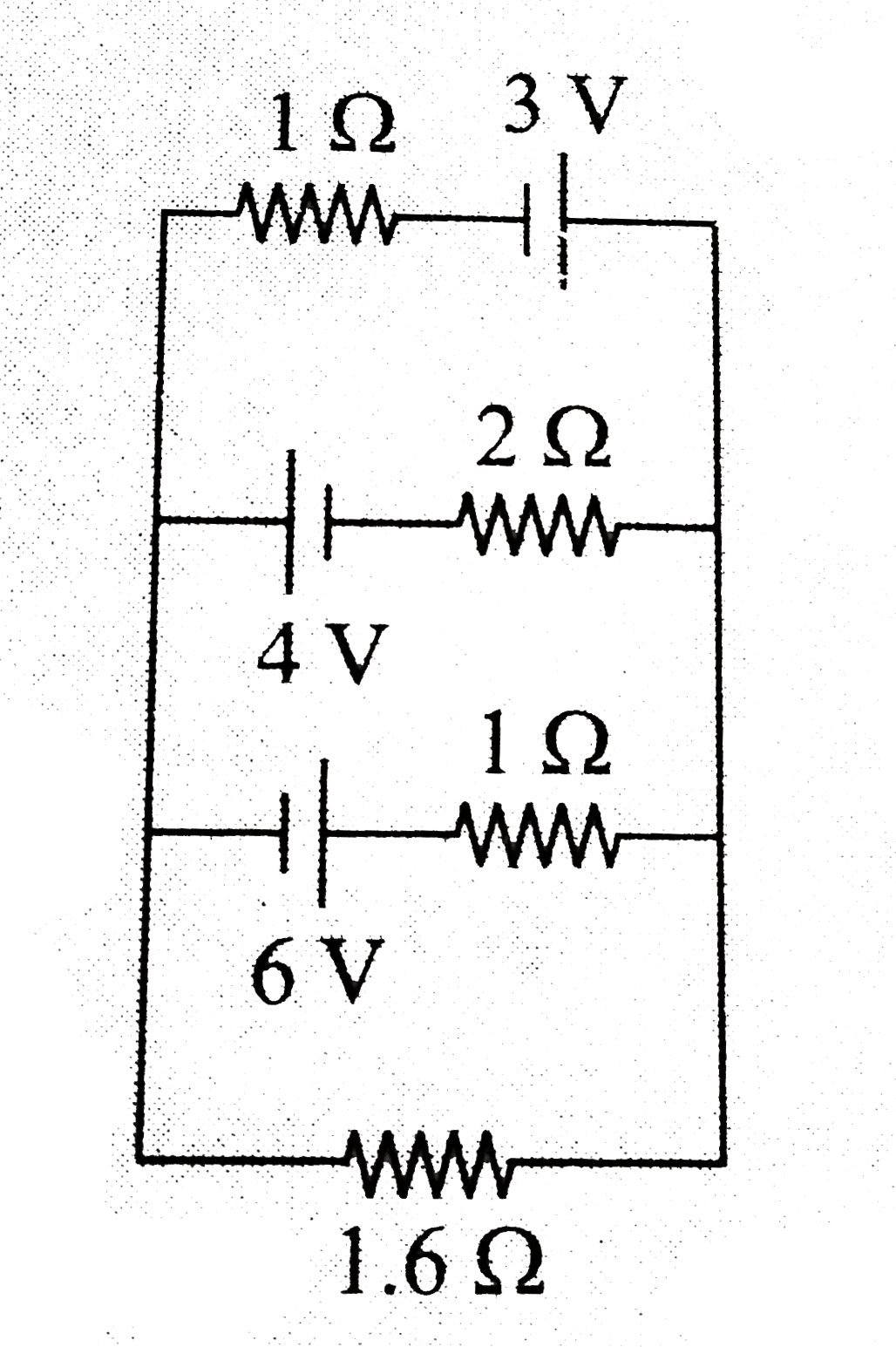
View Solution
