In the given figure, O is the centre of the circle. Prove that
∠XOZ=2(∠XZY+∠YXZ).

Video Solution
Text Solution
Join OY .
Now, are XY subtends ∠XOY at the centre and ∠XZY at a point Z on the remaining part of the circle.
∴∠XOY=2∠XZY ....(i)
Similarly , are YZ subtends ∠YOZ at the centre and ∠YXZ at a point X on the remaining partof the circle.
∴∠YOZ=2∠YXZ ....(ii)
Adding (i) and (ii), we get
∠XOY+∠YOZ=2(∠XZY+∠YXZ)
⇒∠XOZ=2(∠XZY+∠YXZ)
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. The value of x is
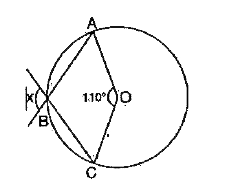 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figure, O is the centre of the circle. Then ∠AED measure
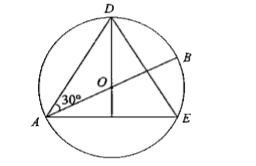 A30∘B45∘C60∘D90∘
A30∘B45∘C60∘D90∘In the given figures, value of y (O is the centre of the circle) is
 A100∘B120∘C130∘D140∘
A100∘B120∘C130∘D140∘
In Figure, O is the centre of the circle, prove that ∠x=∠y+∠z
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn the figure, O is the centre of the circle. Prove ∠AOC=∠AFC+∠AEC.
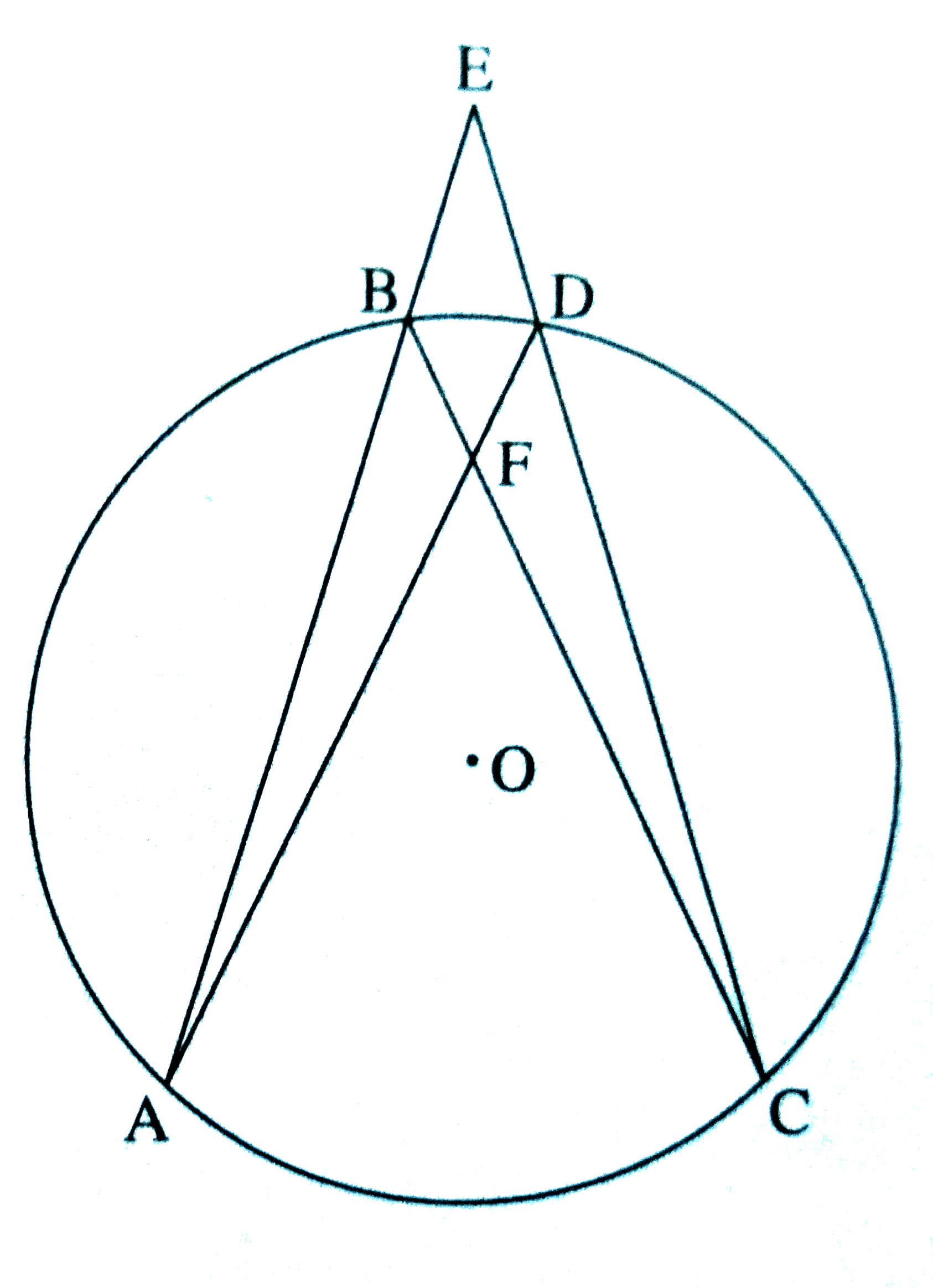
View SolutionIn the adjoining figure, P is the centre of the circle. Prove that ∠XPZ=2(∠XZY+∠YXZ).
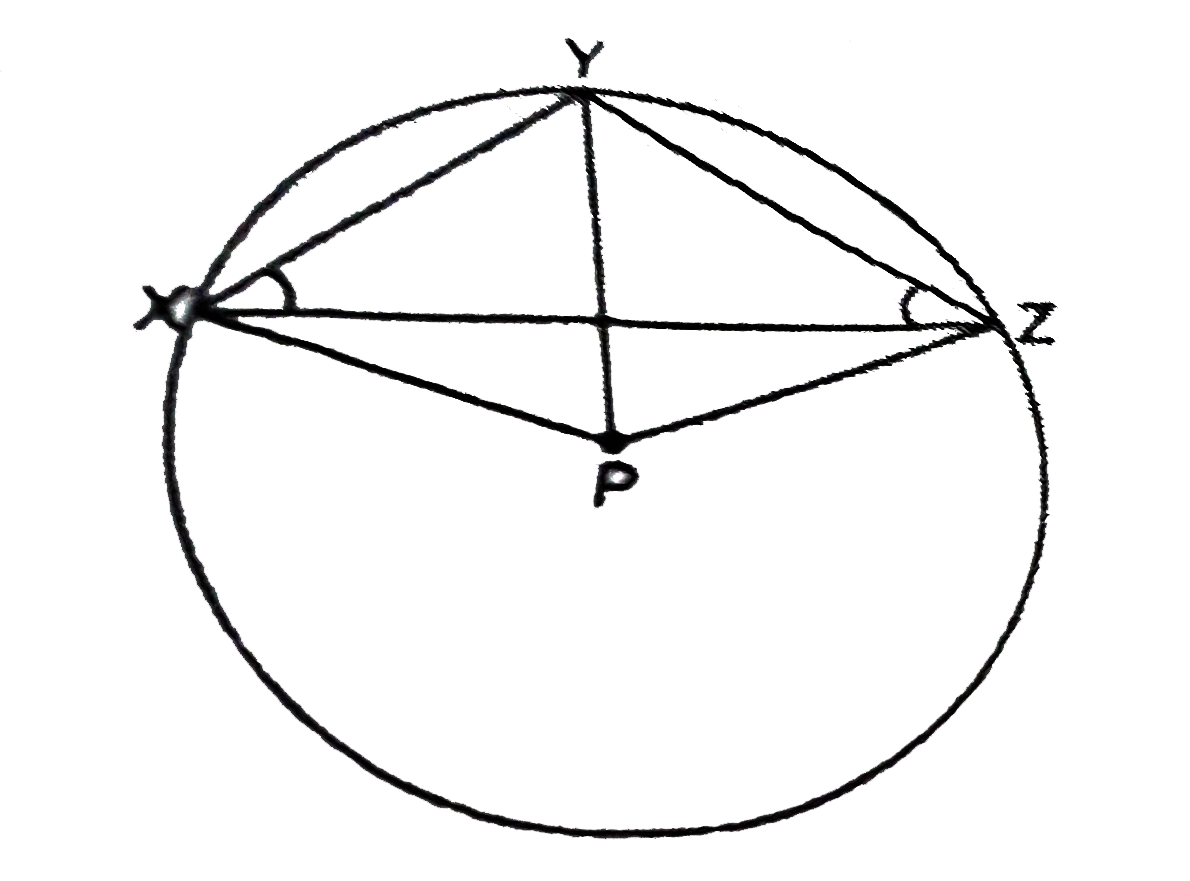
View Solution
