In the adjoining figure, AC is the diameter of a circle with centre O and chord BD⊥AC , intersecting each other at E. Find out the values of p,q,r in terms of x.

(i) Arc AD subtends ∠AOD at the centre and ∠ABD at a point B on the remaining part of the circle.
Now,∠AEB=90∘=x∘2.
Now, ∠AEB=90∘[∵BD⊥AC].
From ΔAEB,we get
p∘=180∘−(∠ABE+∠AEB)
⇒p∘=180∘−(∠ABD+∠AEB)=180∘−(x2+90∘)=(90∘−x∘2)
∴p=90−x2.
(ii) Arc AD subtends ∠AOD at the centre and ∠ACD at a point C of the circle.
∴∠ACD=12∠AOD=x∘2⇒q=x2
(iii) ∠ABC=90∘[ angle in a semicircle ]
⇒∠ABE+∠CBE=90∘⇒∠ABD+∠CBE=90∘
⇒x∘2+∠CBE=90∘⇒∠CBE=(90∘−x∘2)
⇒r=[90−x2].
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A22videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B18videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
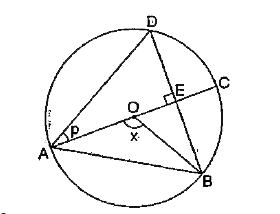 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−x - Question 2 - Select One
In the adjoining figure BD is the diameter of the circle and ∠BCA=41∘. Find ∠ABD:
 A41∘B49∘C22.5∘D20.5∘
A41∘B49∘C22.5∘D20.5∘
In the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
View SolutionIn the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If AC=8cm, BE=2cm, then find the radius of the circle.
 View Solution
View SolutionIn the adjoining figure, AC is the diameter of the circle. If ∠BDC=115∘, then find the value of ∠ACB.
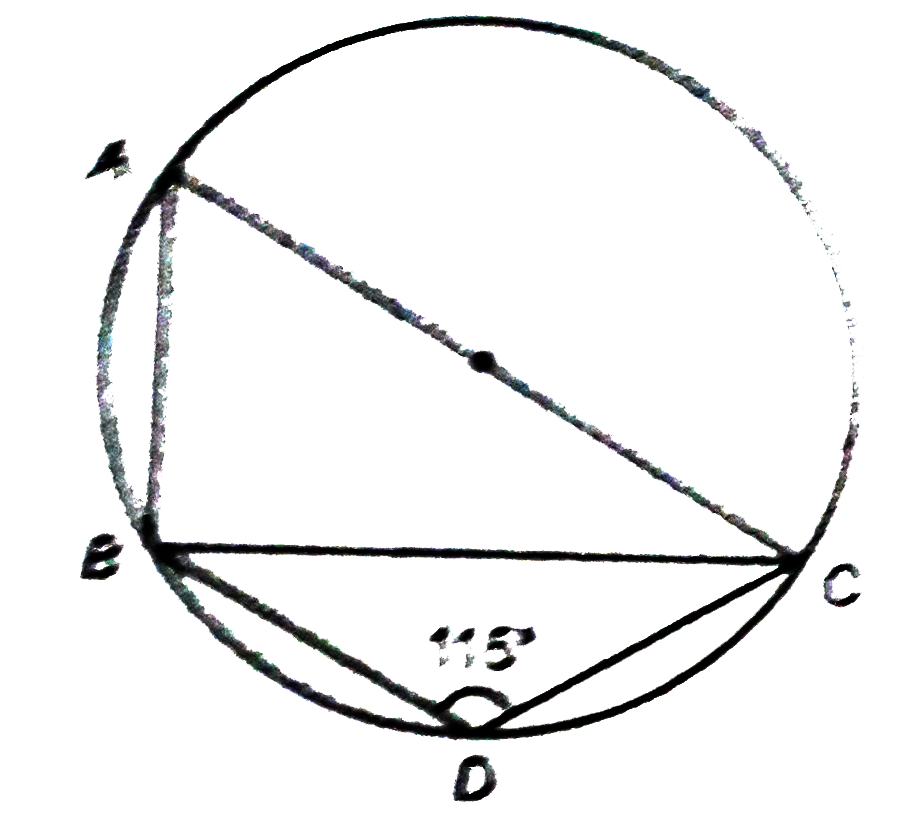 View Solution
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the adjoining figure, AOB is the diameter and O is the centre of the circle. If ∠BDC=60∘, then find the value of ∠ABC.
 View Solution
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
 View Solution
View Solution