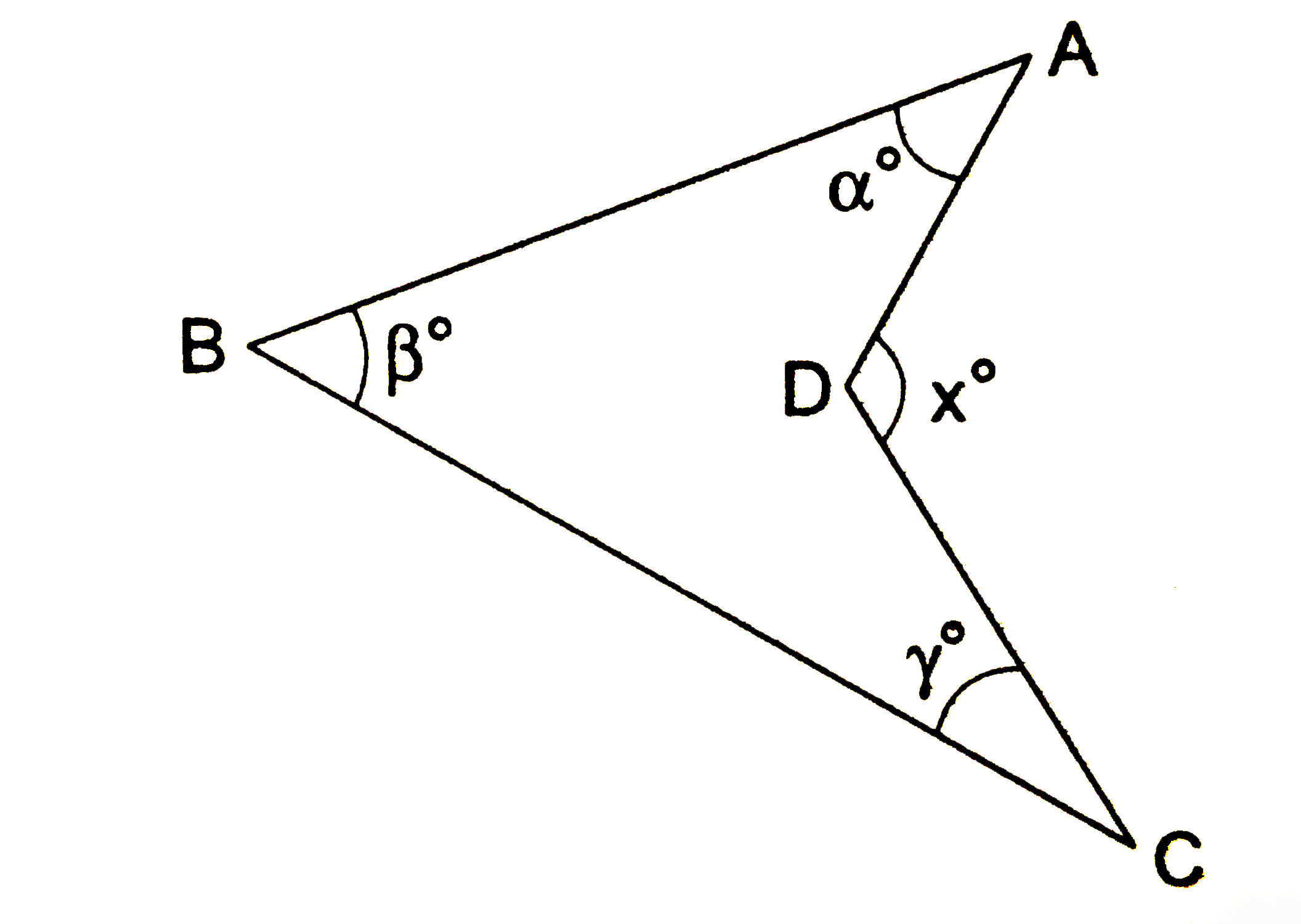
In the given figure, prove that $x = α + β + γ$ .

Video Solution

Text Solution

Verified by Experts

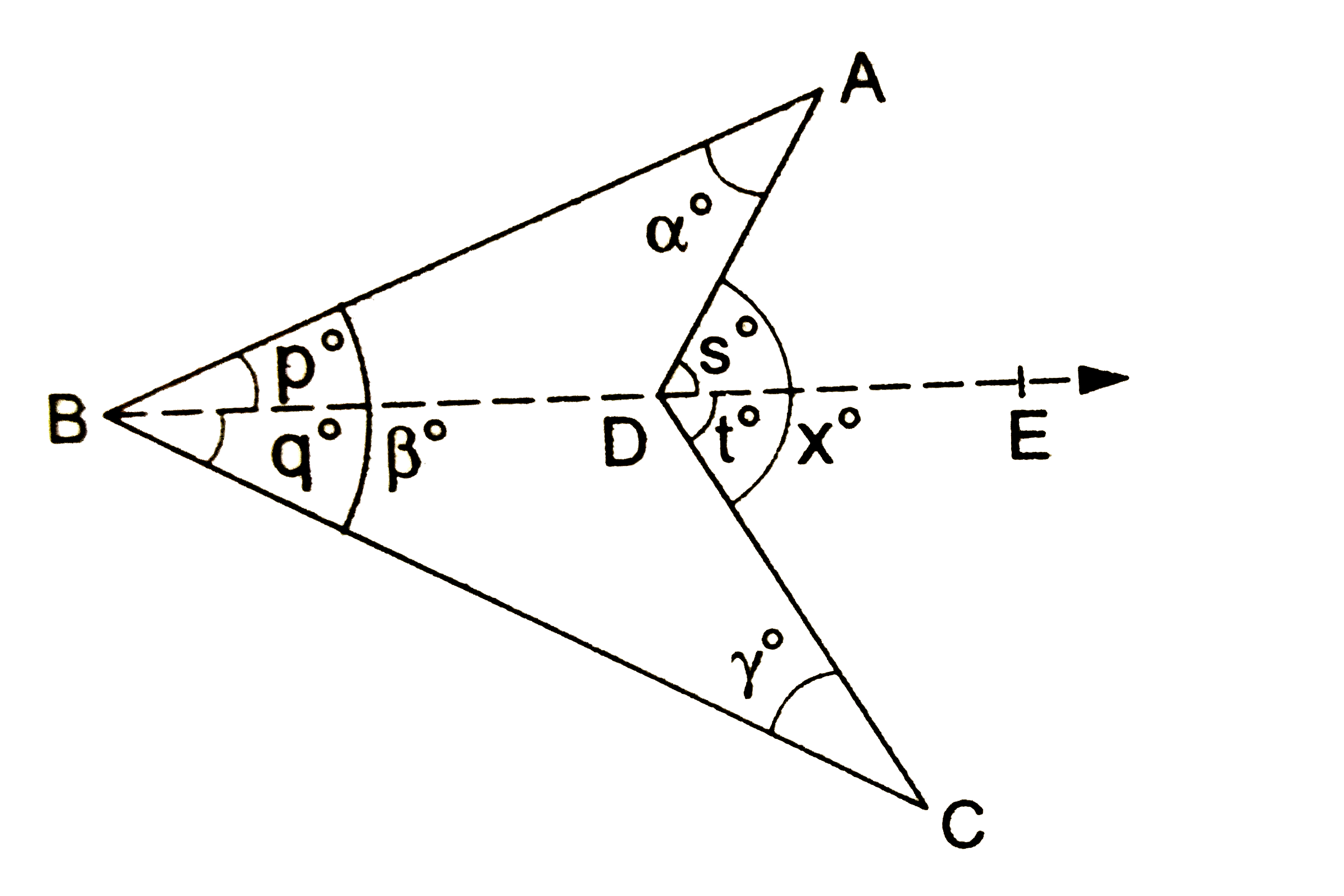
Join B and D and produce BD to E.
Let $∠ A B D = p^{\circ}, ∠ C B D = q^{\circ} and let ∠ A D E = s^{\circ} and ∠ C D E = t^{\circ}$ .
Then, $p + q = β and s + t = x$ .
Now, side BD of $Δ A B D$ has been produced to E.
$∴ s = p + α ... . (i)$
Again, side BD of $Δ C B D$ has been produced to E.
$∴ t = q + γ$ .
Adding the corresponding sides of (i) and (ii), we get
$s + t = (p + q) + α + γ$
$\Rightarrow x = β + α + γ . [∵ s + t = x and p + q = β]$
Hence, $x = α + β + γ$ .

|

Updated on:21/07/2023

Class 9 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$α, β, γ$ are real number satisfying $α + β + γ = π$ . The minimum value of the given expression $sin α + sin β + sin γ$ is
Azero
B $- 3$
Cpositive
Dnegative
Question 2 - Select One
If $α, β, γ$ be the zeros of the polynomial p(x) such that $(α + β + γ) = 3, (α β + β γ + γ α) = - 10 and α β γ = - 24$ then p(x) = ?
A $x^{3} + 3 x^{2} - 10 x + 24$
B $x^{3} + 3 x^{2} + 10 x - 24$
C $x^{3} - 3 x^{2} - 10 x + 24$
Dnone of these
Question 3 - Select One
If $α, β, γ$ are such that $α + β + γ = 2, α^{2} + β^{2} + γ^{2} = 6, α^{3} + β^{3} + γ^{3} = 8$ , then $α^{4} + β^{4} + γ^{4}$ is equal to:
A10
B12
C18
Dnone of these

RS AGGARWAL-TRIANGLES-EXAMPLE

Home
Ask Doubt
Profile