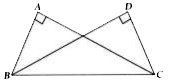
A ΔABC is right angled at A and L is a point on BC such that AL⊥BC. Prove that ∠BAL=∠ACB.
Video Solution
Text Solution
We know that in a right-angled trianlge, the sum of the two acute anlges is 90∘.
So, in right trianlge ΔALB, we have
∠BAL+∠ABL+=90∘⇒∠BAL+∠ABC=90∘ ......(i)
In right triangle BAC, we have
∠ABC+∠ACB=90∘. ....(ii)
From (i) and (ii), we get
∠BAL+∠ABC=∠ABC+∠ACB.
Hence, ∠BAL+∠ACB.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 813videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE16videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)73videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
ΔABC is right angled at A and AD⊥BC. Then BDDC=
A(ABAC)2BABACC(ABAD)2DABAD - Question 2 - Select One
ΔABC is right angled at A. if AB = 24 mm and AC = 7 mm, then BC is
A20 mmB25 mmC30 mmD35 mm
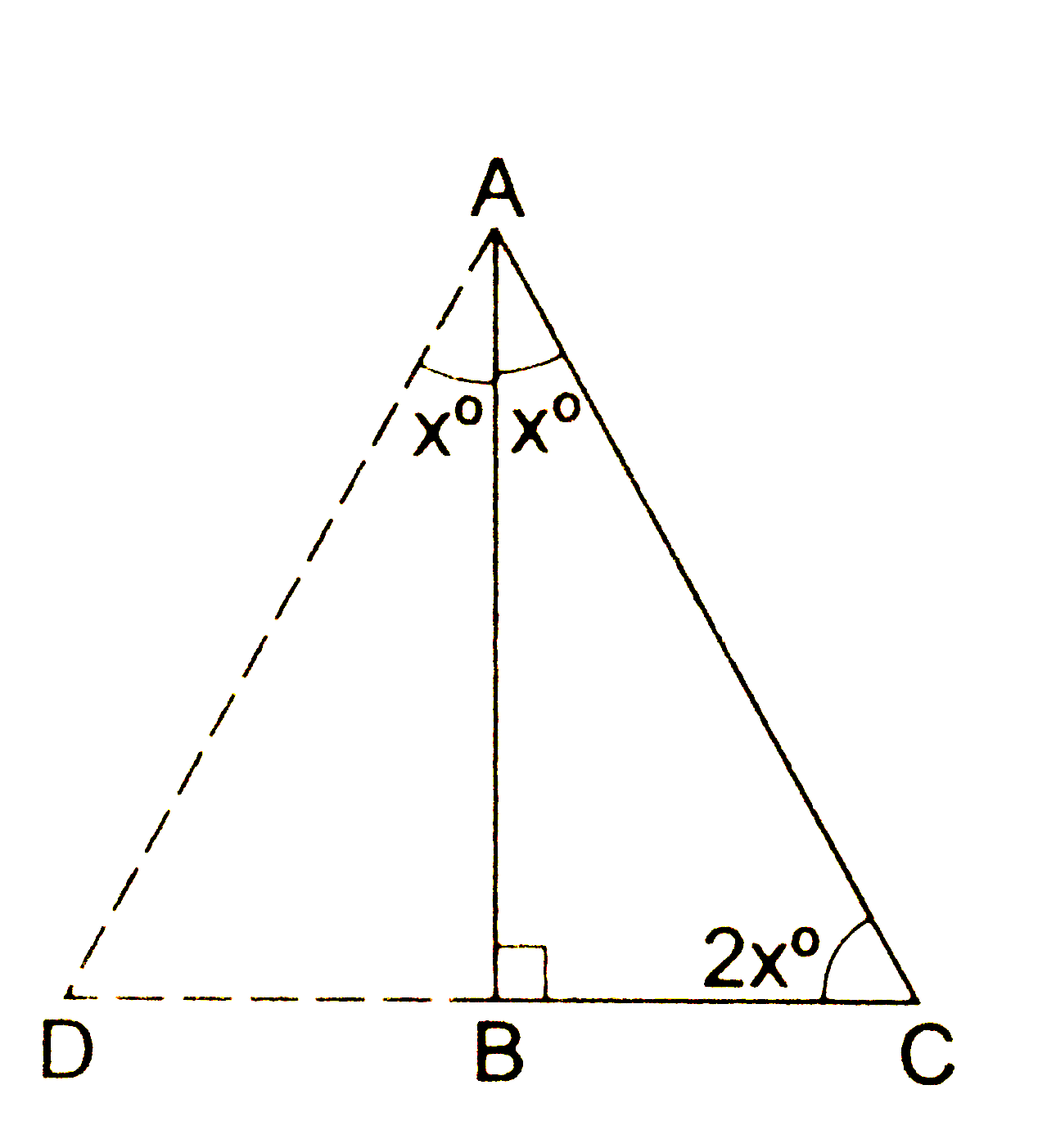
In the given figure, ΔABC is right angled at B such that ∠BCA=2∠BAC. Show that hypotenuse AC = 2BC.
 View Solution
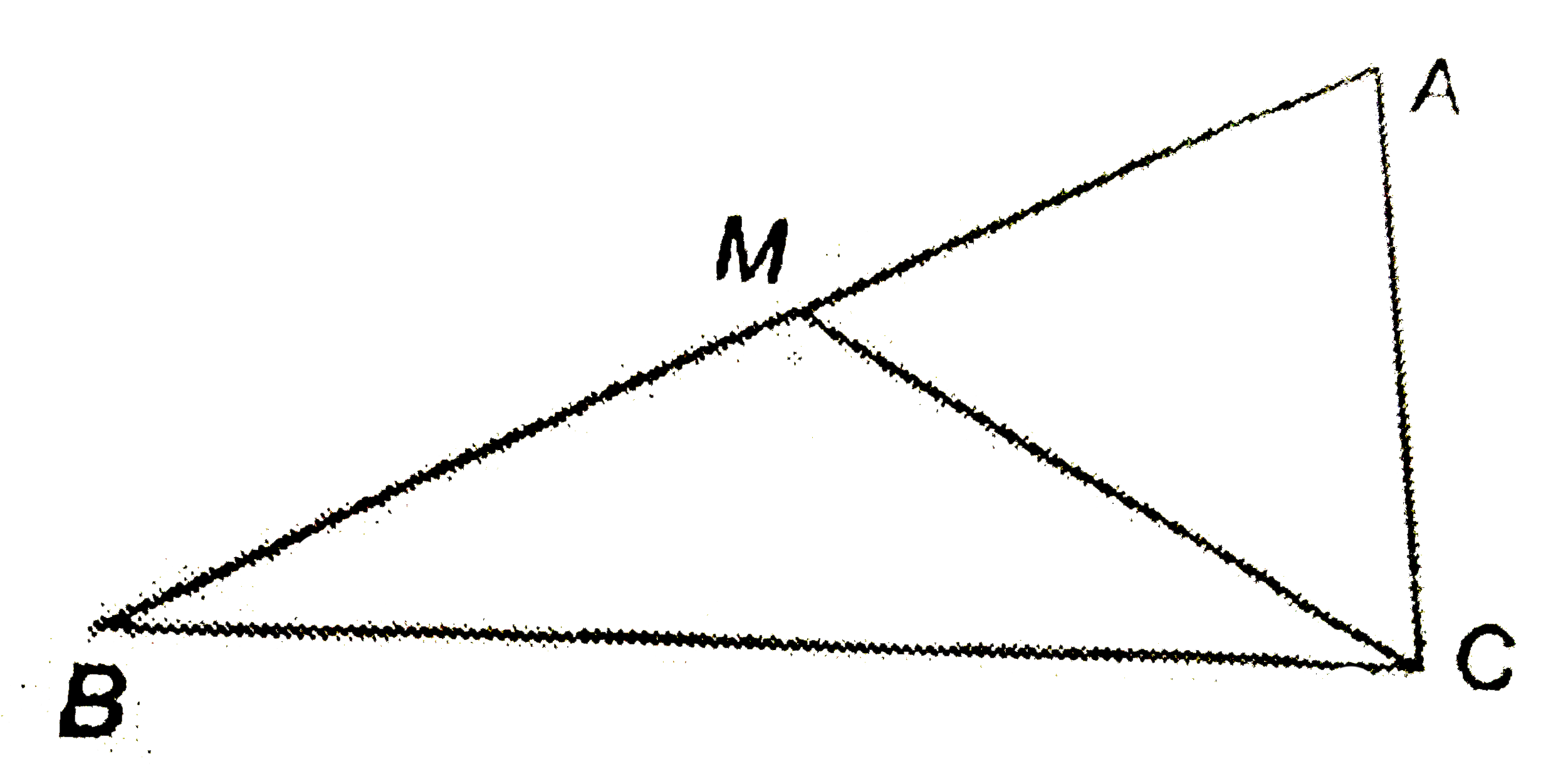
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
 View Solution
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
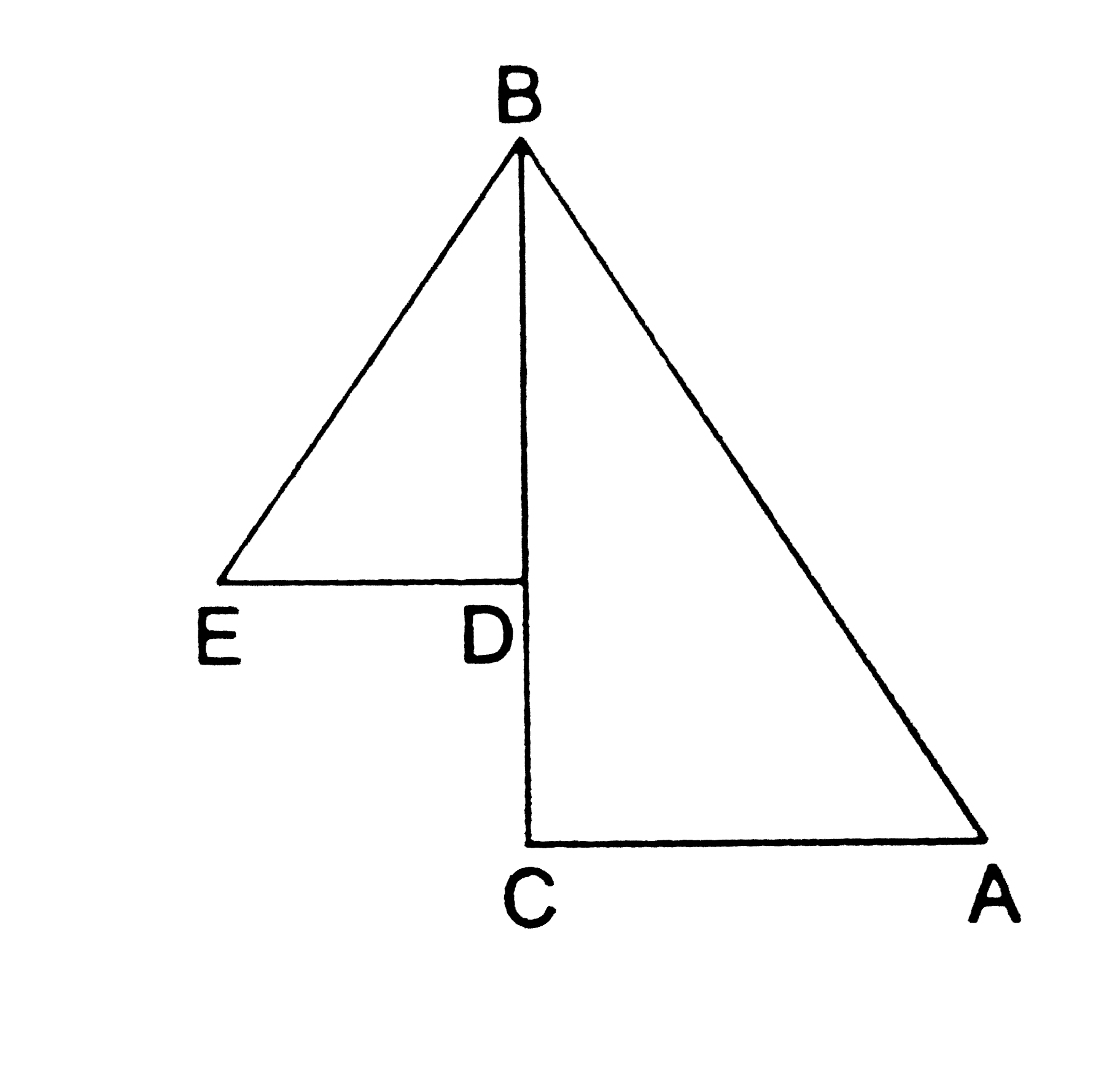 View Solution
View SolutionIn ΔABC , right - angled at B , AB = 24 cm , BC = 7 cm .
sinA,cosAView SolutionIn ΔABC, right angled at B, AB = 5 cm and ∠ACB==30∘. Find BC and AC.
View SolutionIn ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View Solution