In the given figure, lines AB and CD intersect at a point P such that ∠PAC=45∘,∠ACP=100∘and∠PBD=65∘.Find ∠CPA,∠DPBand∠BDP
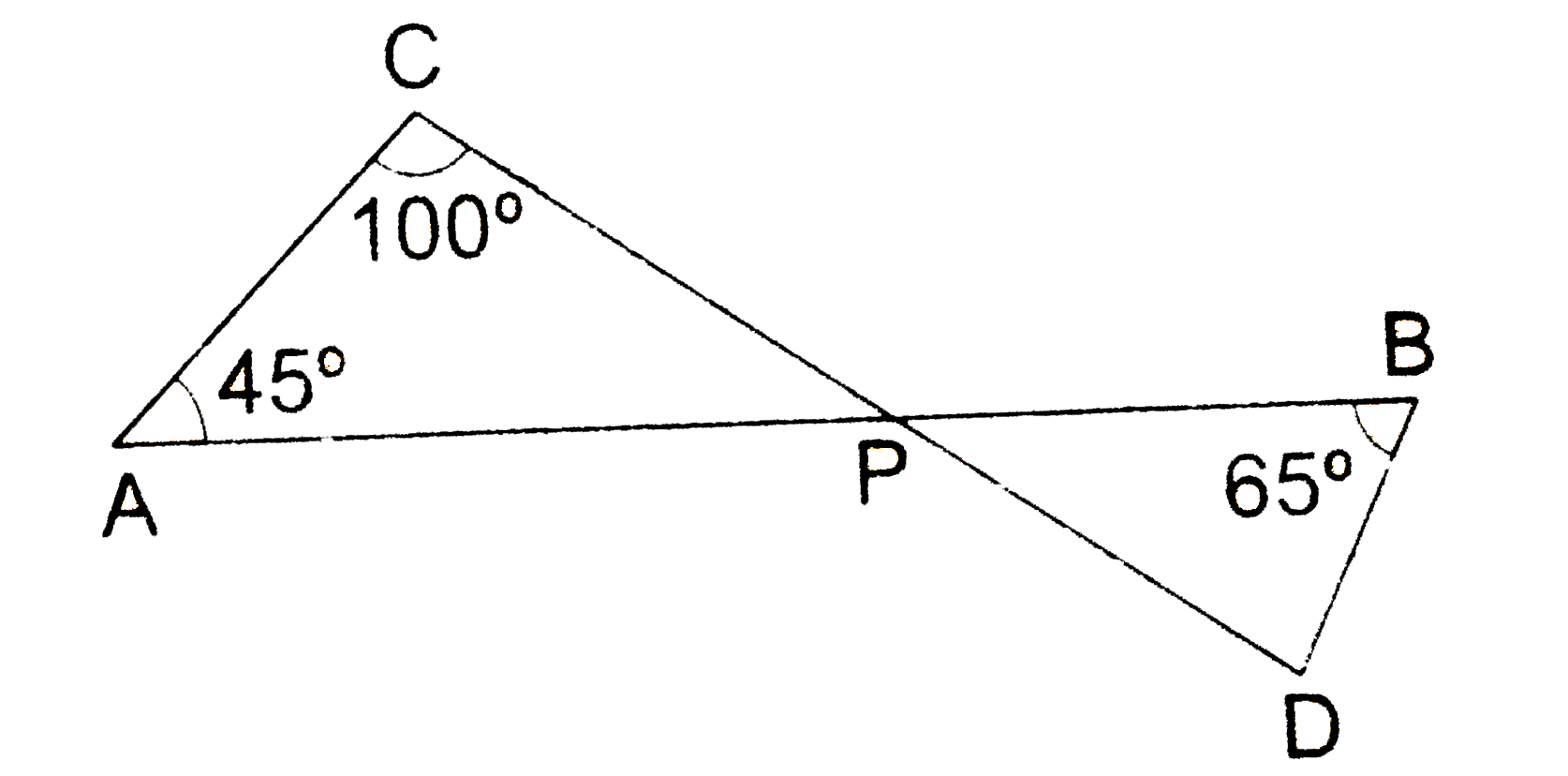
Video Solution
Text Solution
We know that the sum of the angles of triangle is 180∘. In ΔACP, we have
∠PAC+∠ACP+∠CPA=180∘
⇒45∘+100∘+∠CPA=180∘
⇒∠CPA=(180∘−145∘)=35∘
∴∠DPB=∠CPA=35∘ [vertically opp.∠s]
In ΔPBD we have
∠DPB+∠PBD+∠BDP=180∘
[sum of the angles of a triangle]
=35∘+65∘+∠BDP=180∘
⇒∠BDP=(180∘−100∘)=80∘
Hence, ∠CPA=35∘,∠DPB=35∘and∠BDP=80∘.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 813videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE16videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)73videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure , AB∣∣CD. Find x.
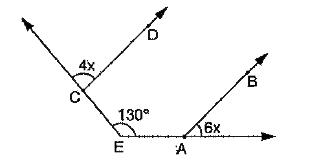 A26∘B13∘C23∘D46∘
A26∘B13∘C23∘D46∘
In the given figure, the two lines AB and CD intersect at a point O such that ∠BOC=125∘. Find the values of x, y, and z.
View SolutionIn the given figure, name:

lines whose point of intersection is PView SolutionIn the given figure, two straight lines AB and CD intersect at a point such that ∠AOC=50∘. Find: (i) ∠BOD
(ii) ∠BOC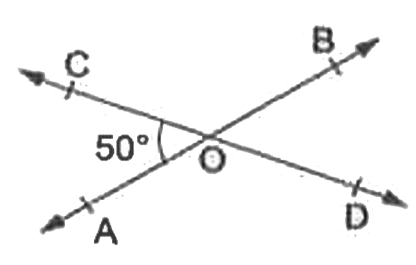 View Solution
View SolutionTwo lines AB and CD intersect each other at a point O such that ∠AOC:∠AOD=5:7. Find all the angles.
View SolutionIn the given figure, AB || DE. Find the length of CD.
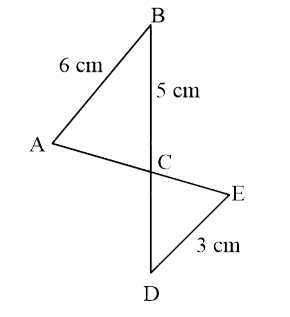 View Solution
View SolutionIn the given figure, AB∣∣CD. Find the value of x.
 View Solution
View SolutionIn the given figure, AB∣∣CD. Find the value of x.
 View Solution
View Solution

