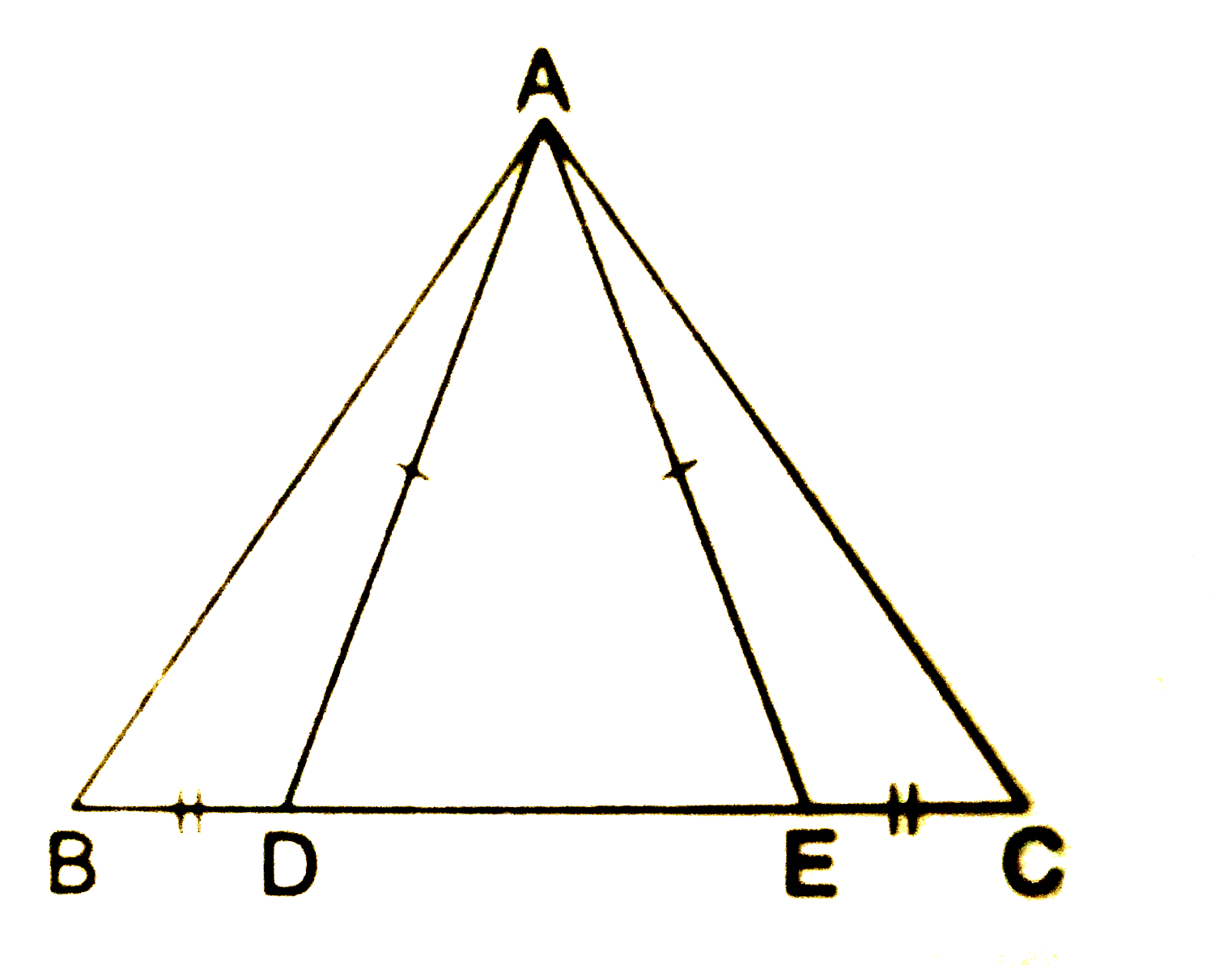
In the given figure, side BC of ΔABC is produced to form ray BD and CE∣∣BA. Show that ∠ACD=∠A+∠B. Deduce that ∠A+∠B+∠C=180∘.
Video Solution
Text Solution
CE∣∣BAandAC is the transversal.
∴∠ACE=∠A ....(i) [alternate interio∠s].
Again, CE∣∣BAandBD is the transversal.
∴∠ECD=∠B ....(ii) [corresponding∠s]
From (i) and (ii), we get
∠ACE+∠ECD=∠A+∠B
∴∠ACD=∠A+∠B
⇒∠A+∠B+∠C=∠ACD+∠ACB
= a straight angle =180∘
Hence, ∠ACD=∠A+∠Band∠A+∠B+∠C=180∘.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 813videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE16videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)73videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
The side BC of Δ ABC is produced to D. If ∠ACD=108∘ and ∠B=12∠A then ∠A is
A36∘B72∘C108∘D59∘ - Question 2 - Select One
In a ΔABC,∠A+∠B=65∘and∠B+∠C=140∘. Find the angles.
A∠A=40∘,∠B=35∘and∠B=35∘and∠C=115∘.B∠A=40∘,∠B=25∘and∠B=25∘and∠C=115∘.C∠A=40∘,∠B=25∘and∠B=25∘and∠C=125∘.D∠A=50∘,∠B=25∘and∠B=25∘and∠C=115∘. - Question 3 - Select One
Side BC of △ABC produced to D if ∠ACD=108∘ and ∠B=12∠A then ∠A is
A108∘B59∘C36∘D72∘
From the adjoining figure prove that ∠A+∠B+∠C+∠D+∠E+∠F=360∘
 View Solution
View SolutionIn the given figure, AD is altitude and AE is bisector of angle BAC of ΔABC. Show that ΔDAE=12(∠B−∠C)
 View Solution
View SolutionABCD is a trapezium in which AB||CD and AD=BC (see figure). Show that
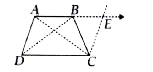
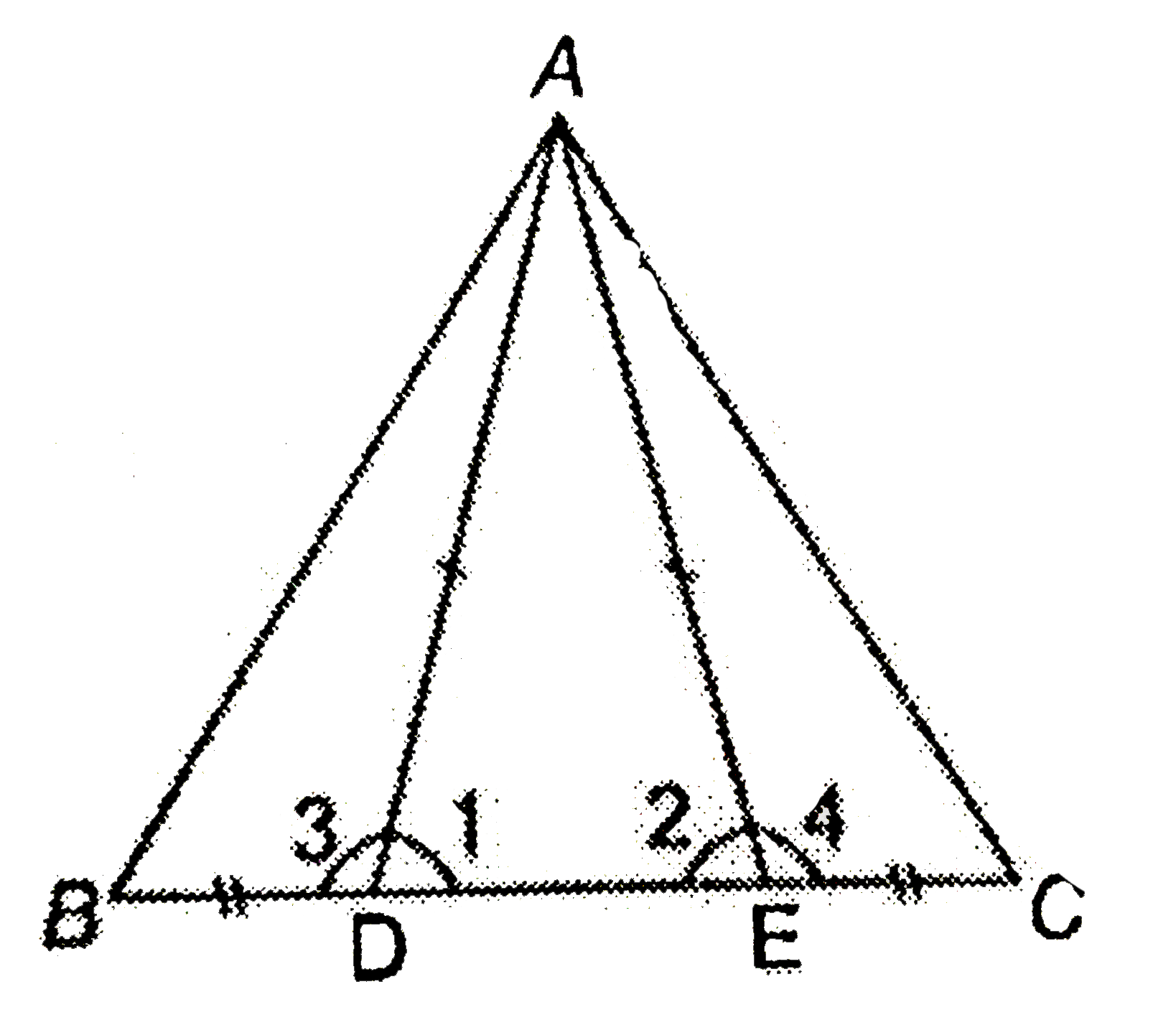
∠A=∠BView SolutionIn the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
 View Solution
View SolutionIn ΔABC,2∠A=3∠B=6∠C, then find ∠A.
View Solution