In a ΔABC the sides AB and AC are produced to points D and E respectively. The bisectors of ∠DBCand∠ECB intersect at a point O.
Prove that ∠BOC=(90∘−12∠A).
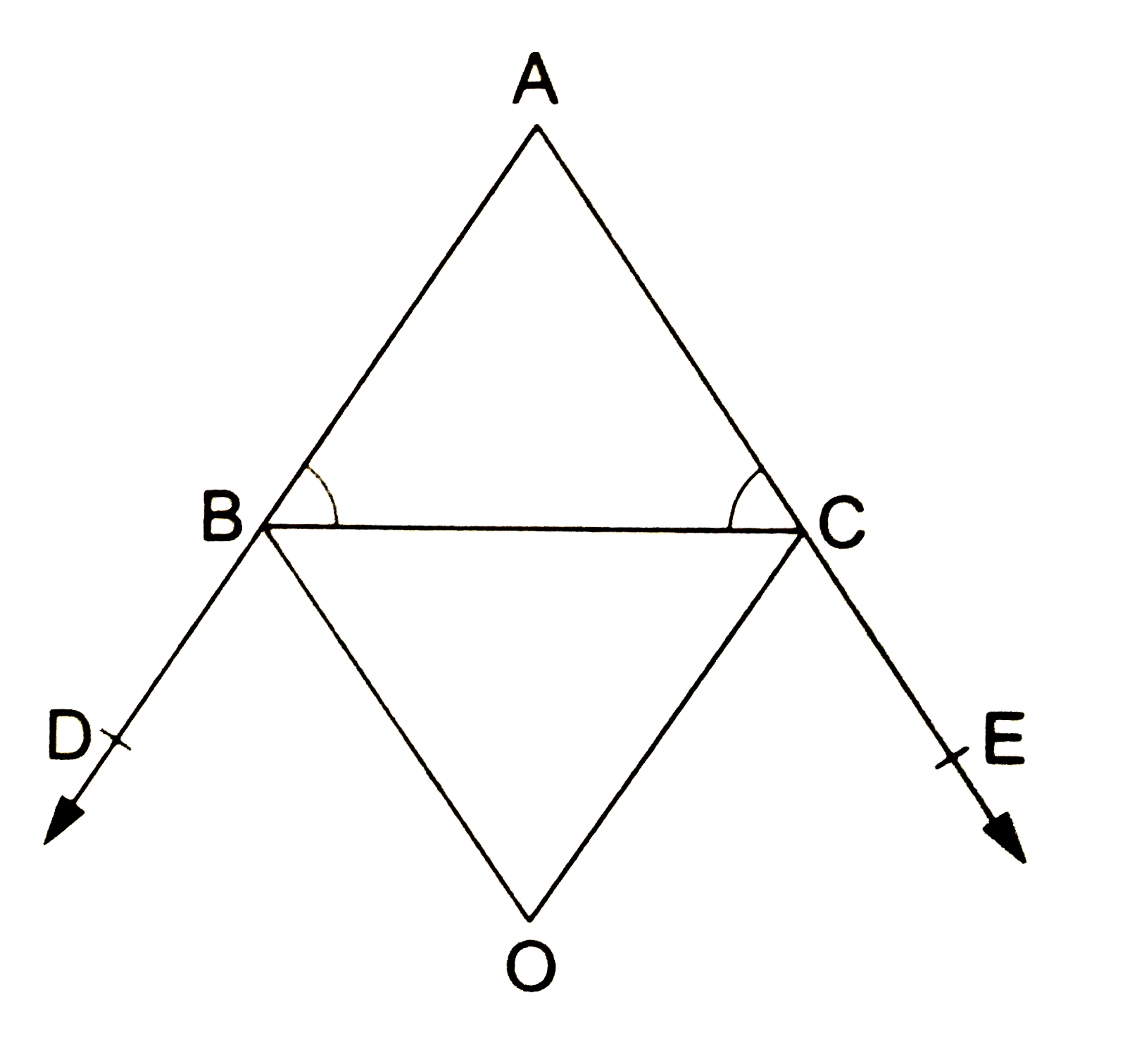
Since ABD is a line, we have
∠B+∠CBD=180∘ [Iinear pair]
⇒12∠B+12∠CBD=90∘
12∠B+∠CBO=90∘
⇒∠CBO=(90∘−12<B) ......(i)
Again, ACE is a straight line.
∴∠C+∠BCE=180∘ [linear pair]
⇒12∠C+12∠BCE=90∘
⇒12∠C+∠BCO=90∘
⇒∠BCO=(90∘−12∠C) ....(ii)
We know that the sum of the angles of a triangle is 180∘. So, from ΔOBC, we get
∠CBO+∠BCO+∠BOC=180∘
⇒(90∘−12∠B)+(90∘−12∠C)+∠BOC=180∘
["using (i) and (ii)"]
⇒180∘−12(∠B+∠C)+∠BOC=180∘
∠BOC=12(∠B+∠C)
∠BOC=12(∠B+∠C)
∠BOC=12(∠A+∠B+∠C)−12∠A
["adding and subtracting 12∠A]
⇒∠BOC=(12×180∘)−12∠A [∵∠A+∠B+∠C=180∘]
⇒∠BOC=(90∘−12∠A).
n Hence, ∠BOC=(90∘−12∠A).
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 8
13 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)
73 Videos
Similar Questions
Knowledge Check
If ΔABC,∠A=52∘, Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBDand∠BCE meet at point O, then ∠BOC is equal to:
A106∘B64∘C16∘D32∘In a ΔABC, the bisectors of ∠Band∠C intersect each other point O. Then∠BOC is ?
A∠BOC=180∘+12∠A.B∠BOC=90∘+12∠A.C∠BOC=180∘−12∠A.D∠BOC=90∘−12∠A.
In ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12A
View SolutionIn ΔABC,AB=AC and the bisectors of angles B and C intersect at point O. Prove that
BO=OC
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionIn Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that ∠BOC=90∘−12∠BAC.
View Solution
