An amount of heat passing through a metallic rod in time t is given by Q=KA(T1−T2)tI where k= thermal conductivity
A= Cross sectional area, T1andT2 are temeprature of hot and cold ends respectively and L= length. So the dimesional formula for k=.....Solution in Gujrati
Q=KA(T1−T2)tL is given
∴k=QLA(T1−T2)t....(i)
Where, heat energy [Q]=M1L2T−2
Length [L]=L1
area [A]=L2
differerence of temperature.
(T1−T2)=[ΔT]=K1
time [t]=T1
Note that here we have included K (for temperature) along with M, L and T. Substituting these dimensional formula in equation (1), we get
[k]=M1L2T−2L1L2L1T1=M1L1T−3K−1
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - KUMAR PRAKASHANCHAPTER - UNITS AND MEASUREMENTEXERCISE - SECTION -B (NUMERICALS) (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
1 Video
- UNITS AND MEASUREMENTBOOK - KUMAR PRAKASHANCHAPTER - UNITS AND MEASUREMENTEXERCISE - SECTION -B (NUMERICALS) (QUESTIONS)
29 Videos
- UNITS AND MEASUREMENTBOOK - KUMAR PRAKASHANCHAPTER - UNITS AND MEASUREMENTEXERCISE - SECTION -B (NUMERICALS) (NUMERICAL FROM TEXTUAL EXERCISE)
32 Videos
- THERMODYANMICS BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Question Paper
11 Videos
- WAVESBOOK - KUMAR PRAKASHANCHAPTER - WAVESEXERCISE - SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
23 Videos
Similar Questions
In an experiment, refractive index of glass wavs observed to be 1.54,1.53,1.44,1.54,1.56&1.45, So, its absolute error, relative error & percentage error are ..... ........ & ...... Respectively.
View Solution(a) 1 rad = .... Degree
(b) 1 rad = .... Min
(c) 1 rad = .... Sec
View SolutionThe volume of a cube of side 1 cm is equal to …….m3.
View SolutionWhy is a steam burn more damaging than a burn with boiling water of the same ?
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmospere, find the temperature at B.

View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionA solid body A of mass m and specific heat capacity ‘s’ has temperature T1=400K. It is placed, at time t=0, in atmosphere having temperature T0=300K. It cools, following Newton’s law of cooling and its temperature was found to be T2=350Kat time t0. At time t0, the body A is connected to a large water bath maintained at atmospheric temperature T0, using a conducting rod of length L, cross section A and thermal conductivity k. The cross sectional area A of the connecting rod is small compared to the overall surface area of body A. Find the temperature of A at time t=2t0.
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T_(1) . The other end of the rod is kept at at temperature T_(2) . The thermal conductivity of the material of the rod is K and emissivity of the rod is e . It is given that T_(2)=T_(S)+DeltaT where DeltaT lt lt T_(S) , T_(S) being the temperature of the surroundings. If DeltaT prop (T_(1)-T_(S)) , find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T_(2) .
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = alpha T, where alpha is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T_(1) and T_(2) (T_(1)gtT_(2)) . Heat current flowing through the rod will be
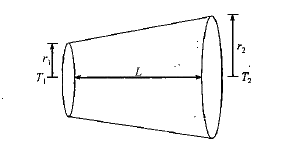
View SolutionFind the heat current through the frustum of a cone shown in figure-4.20. Temperature of its two ends are maintained at T1 and T2(T_(2)>T_(1)) respectively and the thermal conductivity of the material is k.
View Solutionलम्बाई L तथा अनुप्रस्थ - क्षेत्रफल A वाली छड़ का एक सिरा T1 तापमान वाली भट्टी में रखा है | छड़ का दूसरा सिरा ताप T2 पर है | छड़ के पदार्थ की ऊष्मा चालकता K तथा उत्सर्जकताe है | दिया है : T2=Ts+ΔT, जहाँ ΔT<<Ts,Ts वातावरण का तापमान है | यदि ΔT∝(T1−Ts), तो अनुक्रमानुपाती नियतांक का मान ज्ञात कीजिए | मान कीजिए कि ऊष्मा का क्षय, केवल T2 ताप वाले सिरे से विकिरण के रूप में हो रहा है |

View SolutionConstant temperature of ends are T1 and T2 (where T1>T2) for a conducting rod of 'L' length and cross-sectional area A. What would be the rate of heat transfer in thermal steady state ?
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

View SolutionOne end of a rod of length L and cross - sectioal area A is kept in a furance of temperature T_(1) . The other end of the rod is kept at a tempearute T_(2) . The thermal conducitivity of the material of the rod is K and emissivity of rod is K and emissivity of rod is e. It is given that T_(2) = T_(s) + DeltaT , where Delta T lt lt T_(s), T_(s) being the temperature of surroudings. If Delta T prop (T_(1) - T_(s)) , find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T_(2) ..
View Solution
