If A, B, C and D are four points such that ∠BAC=45∘and∠BDC=45∘, then A, B, C and D are concyclic.
The correct Answer is:1
To determine if points A, B, C, and D are concyclic given that ∠BAC = 45° and ∠BDC = 45°, we can follow these steps:
Step 1: Understand the Given Angles
We have two angles:
- ∠BAC = 45°
- ∠BDC = 45°
Step 2: Identify the Segments
Both angles are formed with respect to points B, A, C, and D. We need to analyze the segments in which these angles lie.
Step 3: Recognize the Circle Property
According to the properties of circles, if two angles are subtended by the same chord in the same segment of a circle, then those angles are equal.
Step 4: Apply the Circle Theorem
Since both angles ∠BAC and ∠BDC are equal (both are 45°), we can conclude that they are subtended by the same chord AC in the same segment of the circle.
Step 5: Conclude the Cyclic Nature
Since the angles are equal and subtended by the same chord, we can conclude that points A, B, C, and D lie on the same circle. Therefore, A, B, C, and D are concyclic.
Final Conclusion
Thus, the statement that A, B, C, and D are concyclic is true.
---
We have two angles:
- ∠BAC = 45°
- ∠BDC = 45°
Both angles are formed with respect to points B, A, C, and D. We need to analyze the segments in which these angles lie.
According to the properties of circles, if two angles are subtended by the same chord in the same segment of a circle, then those angles are equal.
Since both angles ∠BAC and ∠BDC are equal (both are 45°), we can conclude that they are subtended by the same chord AC in the same segment of the circle.
Since the angles are equal and subtended by the same chord, we can conclude that points A, B, C, and D lie on the same circle. Therefore, A, B, C, and D are concyclic.
Thus, the statement that A, B, C, and D are concyclic is true.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.320videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
If A, B, C and D are four points such that ∠BAC=30∘and∠BDC=60∘,then D is the centre of the circle through A, B and C.
View SolutionIf ABCD is a square then show that the points, A,B, C and D are concyclic.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points on the sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionA, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
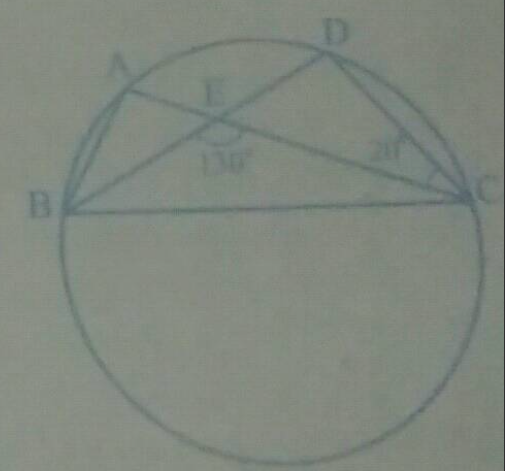
View SolutionA, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC =130∘ and ∠ECD=20∘ Find ∠BAC∘
 View Solution
View SolutionIn Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC\ =\ 130o and ∠ECD\ =\ 20⊙ Find ∠BAC.
View SolutionA,B,C,D are any four points, prove that →AB.→CD+→BC.→AD+→CA.→BD=0.
View SolutionIf A,B,C,D are four distinct point in space such that −−→AB is not perpendicular to −−→CD and satisfies −−→AB.−−→CD=k(∣∣∣−−→AD∣∣∣2+∣∣∣−−→BC∣∣∣2−∣∣∣−−→AC∣∣∣2−∣∣∣−−→BD∣∣∣2), then find the value of k.
View SolutionIf A,B,C,D are four distinct point in space such that AB is not perpendicular to CD and satisfies →AB.→CD=k(∣∣→AD∣∣2+∣∣→BC∣∣2−∣∣→AC∣∣2=∣∣→BD∣∣2), then find the value of k.
View SolutionIf a, b, c and d are four coplanr points, then prove that [abc]=[bcd]+[abd]+[cad].
View Solution

