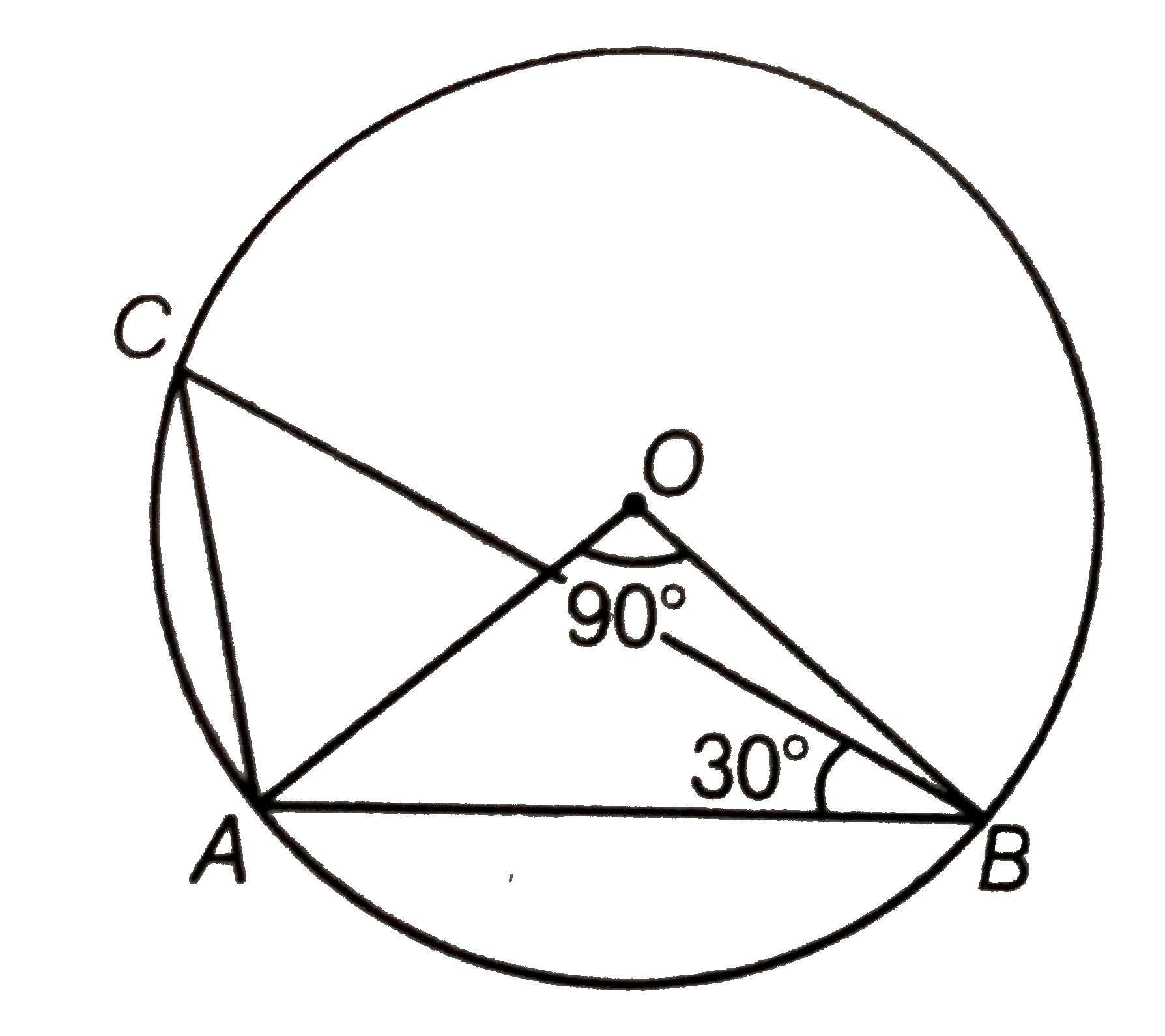
In figure, if AOB is a diameter and ∠ADC=120∘,then∠CAB=30∘.
The correct Answer is:1
Join CA and CB.
Since, ADCB is a cyclic quadrilateral.
∴∠ADC+∠CBA=180∘.
[sum of opposite angles of cyclic quadrilateral is 180∘]
⇒∠CBA=180∘−120∘=60∘[∵∠ADC=120∘]
InΔACB,∠CAB+∠CBA+∠ACB=180∘
[by angle sum property of a triangle]
∴∠CAB+60∘+90∘=180∘
[triangle formed from diameter to the circle is 90∘i.e.,∠ACB=90∘]
⇒∠CAB=180∘−150∘=30∘
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.320videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
In figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
 View Solution
View SolutionIn figure, if ∠AOB=90∘and∠ABC=30∘, then∠CAO is equal to
 View Solution
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral . If ∠CBX=104∘ and ∠CAB=56∘, then find the value of ∠ADB.
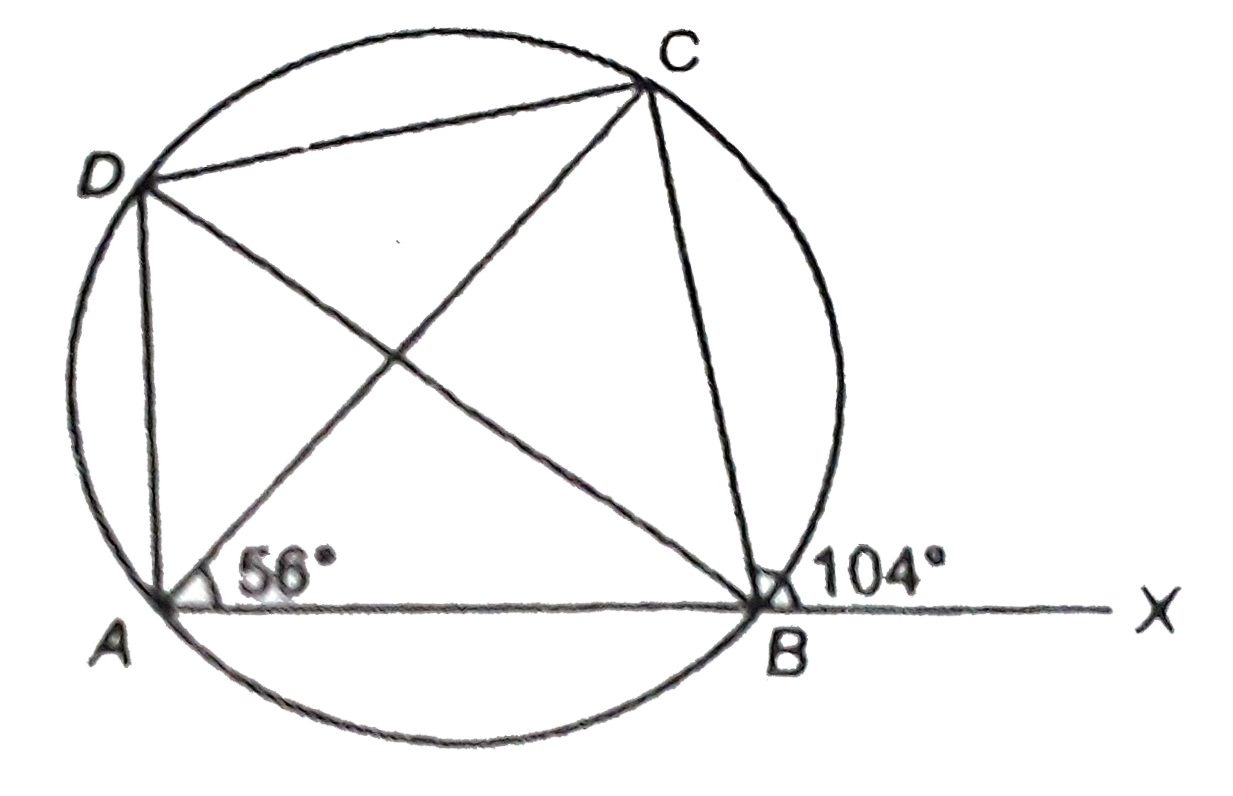 View Solution
View SolutionIn the given figure, C and D are points on the semi circle described on AB as diameter. Given angle BAD=70∘ and angle DBC=30∘, calculate angle BDC
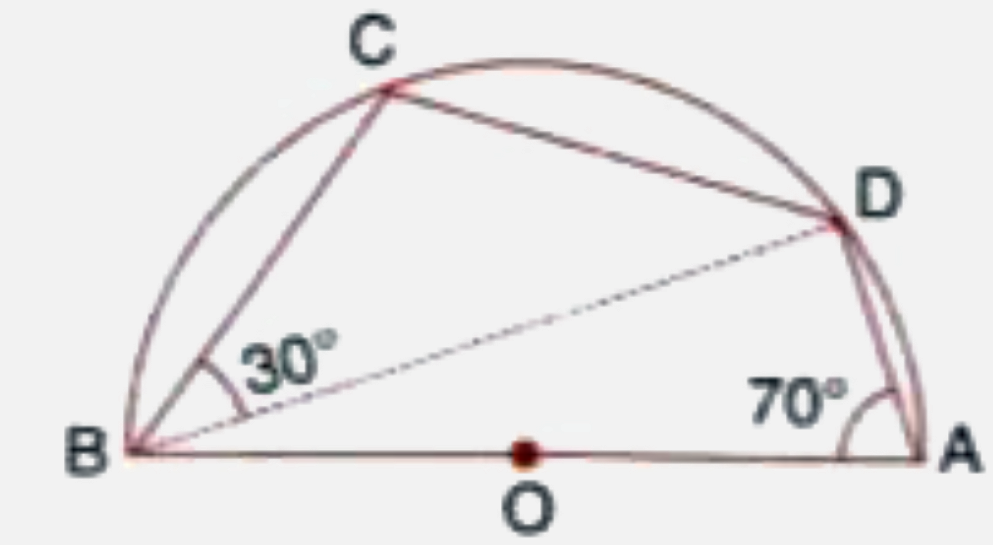 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
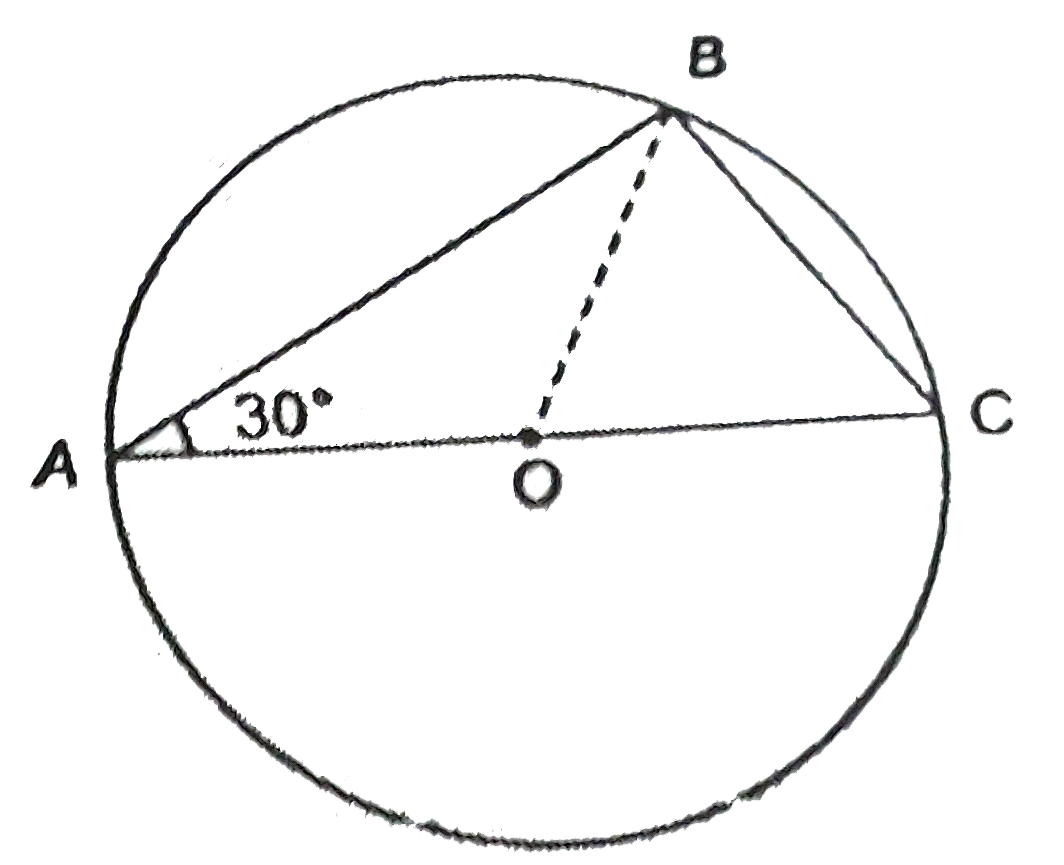 View Solution
View SolutionIf AOB is a diameter of the circle and AC=BC, then ∠CAB is equal to
View SolutionIn the adjoining figure, AD is the diameter of the circle and ∠BCD=140∘. Find the value of ∠ADB.
 View Solution
View SolutionIn the adjoining figure, if ∠ACB=40∘, ∠DPB=120∘, then find ∠CBD.
 View Solution
View SolutionIn the adjoining figure, AOB is the diameter of the circle. If ∠ABP=45∘, then find the value of ∠PQB.
 View Solution
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
View Solution

