In figure, if ∠1=∠2 and ΔNSQ=ΔMTR, then prove that ΔPTS~ΔPRQ.
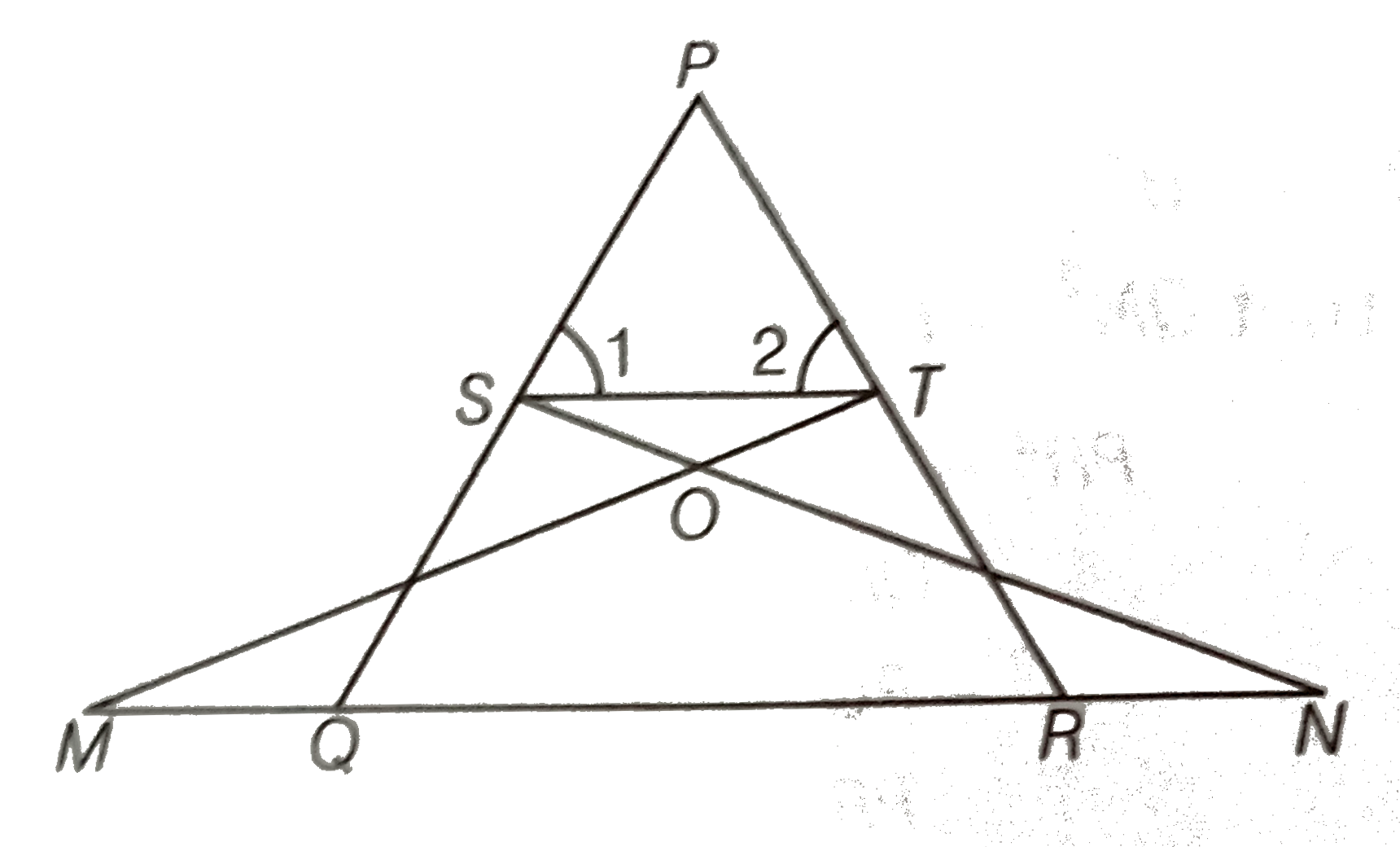
Given ΔNSQ≅ΔMTRand∠1=∠2
to prove ΔPTS~ΔPRQ
Proof Since, ΔNSQ≅ΔMTR
So, SQ=TR…..(i)
Also, ∠1=∠2⇒PT=PS..(ii)
[since, sides opposite to equal angles are also equal]
From Eqs. (i) and (ii) PSSQ=PTTR
⇒ST||QR [by convense of basic proportionality theorem]
∴∠1=∠PQR
and ∠2=∠PRQ
in ΔPTSandΔPRQ [common angles]
∠P=∠P
∠1=∠PQR
∠2=∠PRQ
∴ΔPTS~ΔPRQ [by AAA similarity criterion]
Hence proved
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions18videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
In the following figure, ∠A=∠C and AB = BC.
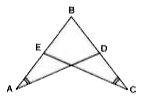
Prove that : ΔABD≅ΔCBEView SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
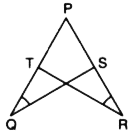 View Solution
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
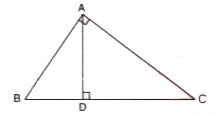
Prove that : ΔABD is similar to ΔCAD.View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.
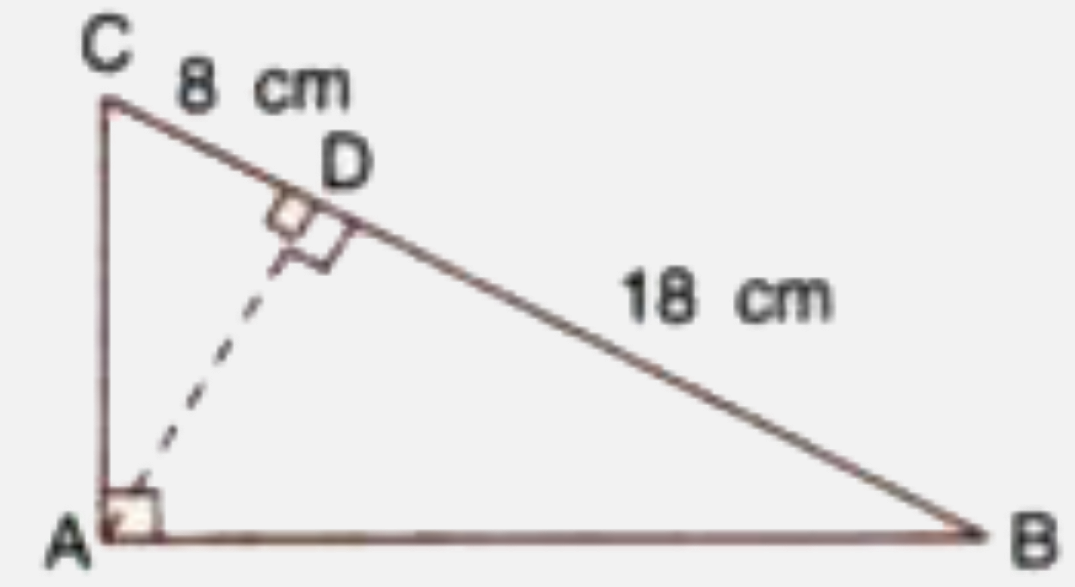
Prove that : ΔADB~ΔCDA.View SolutionIn the given figure , BC = CE and ∠1=∠2.
Prove that :
ΔGCB=ΔDCB .
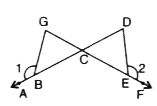 View Solution
View SolutionIn the adjoining figure, we have ∠1=∠2and=∠3. Show that ∠1=∠3.
 View Solution
View SolutionIn the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
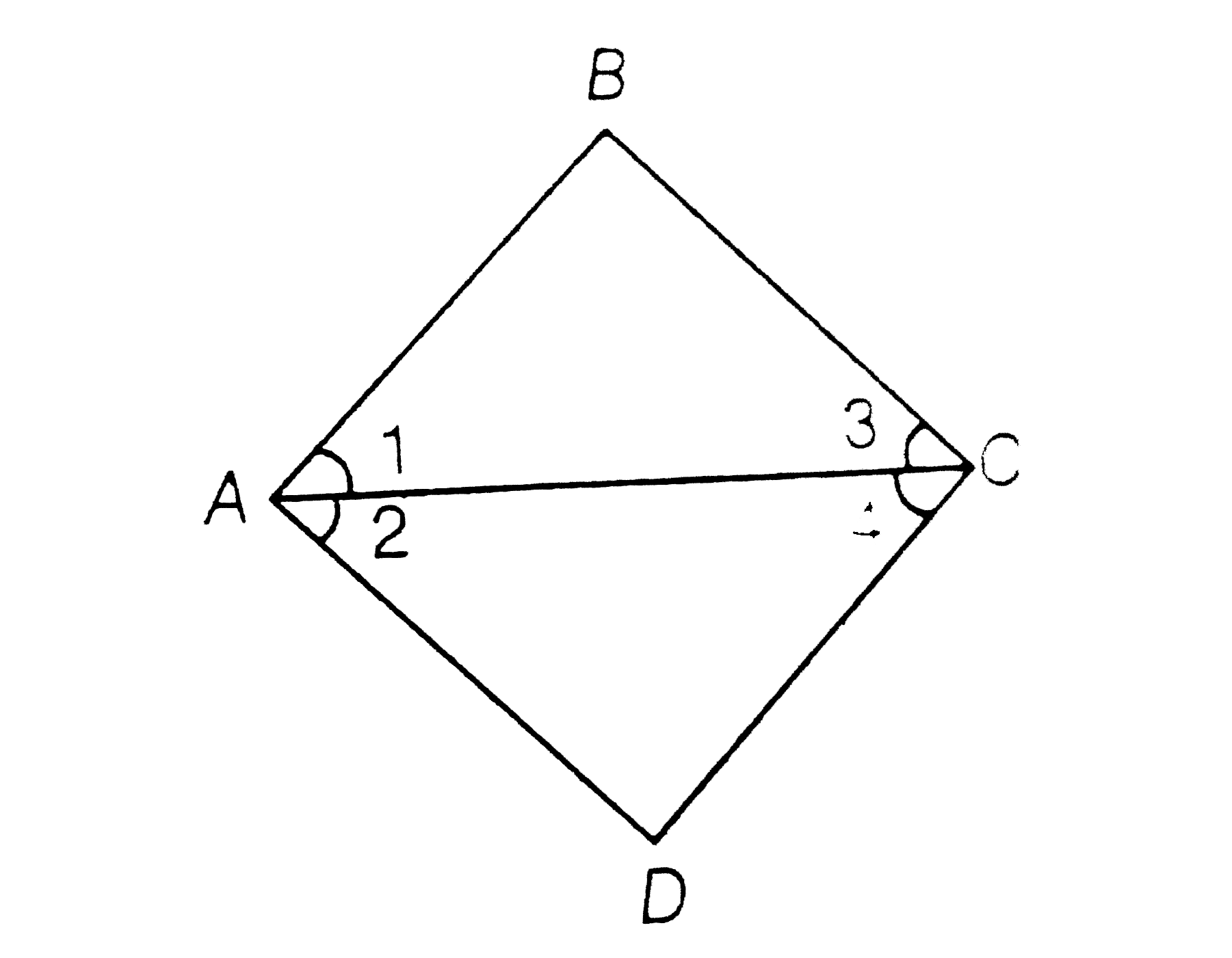 View Solution
View SolutionIn the given figure, AD = DB = DE ∠EAC=∠FACand∠F=90∘
Prove that
(i) ∠AEB=90∘
(ii) ΔCEG is isosceles.
(iii) ∠CEG=∠EAF
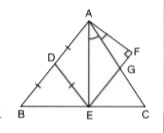 View Solution
View SolutionIn the given figure, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that ∠AMD=90∘.
 View Solution
View SolutionIn Figure, m∣∣n and angles 1 and 2 are in the ratio 3:2. Determine all the angles from 1 to 8.
View Solution

