Find the value of x for which DE||AB in given figure.
To find the value of x for which DE∥AB in the given figure, we can use the Basic Proportionality Theorem (also known as Thales' theorem). Here’s a step-by-step solution:
Step 1: Set up the proportion
Since DE∥AB, we can use the Basic Proportionality Theorem which states that:
CDAD=CEBE
Given:
- CD=x+3
- AD=3x+19
- CE=x
- BE=3x+4
Step 2: Write the equation
Substituting the values into the proportion gives:
x+33x+19=x3x+4
Step 3: Cross-multiply
Cross-multiplying gives us:
(x+3)(3x+4)=x(3x+19)
Step 4: Expand both sides
Expanding both sides:
- Left side:
x(3x)+4x+9+12=3x2+4x+9
- Right side:
3x2+19x
So, we have:
3x2+4x+12=3x2+19x
Step 5: Rearrange the equation
Now, we can move all terms to one side:
3x2+4x+12−3x2−19x=0
This simplifies to:
−15x+12=0
Step 6: Solve for x
Rearranging gives:
−15x=−12
Dividing both sides by -15:
x=1215=45
Step 7: Conclusion
Thus, the value of x is:
45
Since DE∥AB, we can use the Basic Proportionality Theorem which states that:
CDAD=CEBE
Given:
- CD=x+3
- AD=3x+19
- CE=x
- BE=3x+4
Substituting the values into the proportion gives:
x+33x+19=x3x+4
Cross-multiplying gives us:
(x+3)(3x+4)=x(3x+19)
Expanding both sides:
- Left side:
x(3x)+4x+9+12=3x2+4x+9
- Right side:
3x2+19x
3x2+4x+12=3x2+19x
Now, we can move all terms to one side:
3x2+4x+12−3x2−19x=0
This simplifies to:
−15x+12=0
Rearranging gives:
−15x=−12
Dividing both sides by -15:
x=1215=45
Thus, the value of x is:
45
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions18videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
Find the length of AB for the given ΔABC.
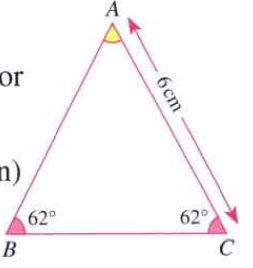 View Solution
View SolutionIn the given figure, AB∣∣CD. If ∠BAC=(3x+15)∘and∠ACD=(2x+45)∘, find the value of x. Also, find the measures of ∠BAC∠ACD
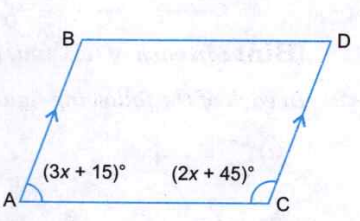 View Solution
View SolutionIn the figure, ABCDE is a pentagon with BE∣∣CD and BC∣∣DE. BC is perpendicular to CD. AB= 5cm, AE=5cm, BE= 7cm, BC= x-y and CD= x+y. If the perimeter of ABCDE is 27cm. find the value of x and y, given x,y,≠0
View SolutionIn Fig. 6.28, find the values of x and y and then show that AB || CD.
 View Solution
View SolutionIn the given figure if DE||BC, find the value of x.
View SolutionIn the given figure, AB and DE are perpendicular to BC. If AB = 6cm, DE = 4cm and AC = 15cm.

(iii) Find the ratio of the area of ΔABC : area of ΔDEC.View SolutionIn the figure if DE||AB, find the value of x . Given AD= (x-4).
DC= 4cm, EB= (3x-19) cm and EC= (x-3) cm.
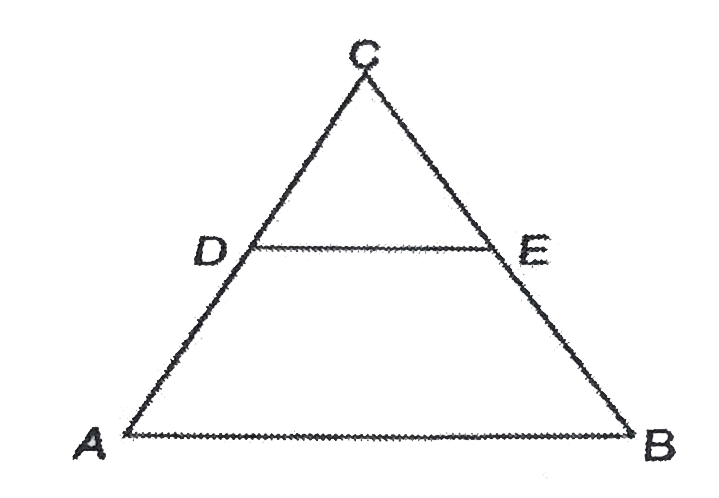 View Solution
View SolutionFind the value of :
6a2b−5ab2+10ab−7 given that a=1andb=2View SolutionFind the RAB in the given network.
 View Solution
View SolutionFind RAB in the circuit shown in figure.
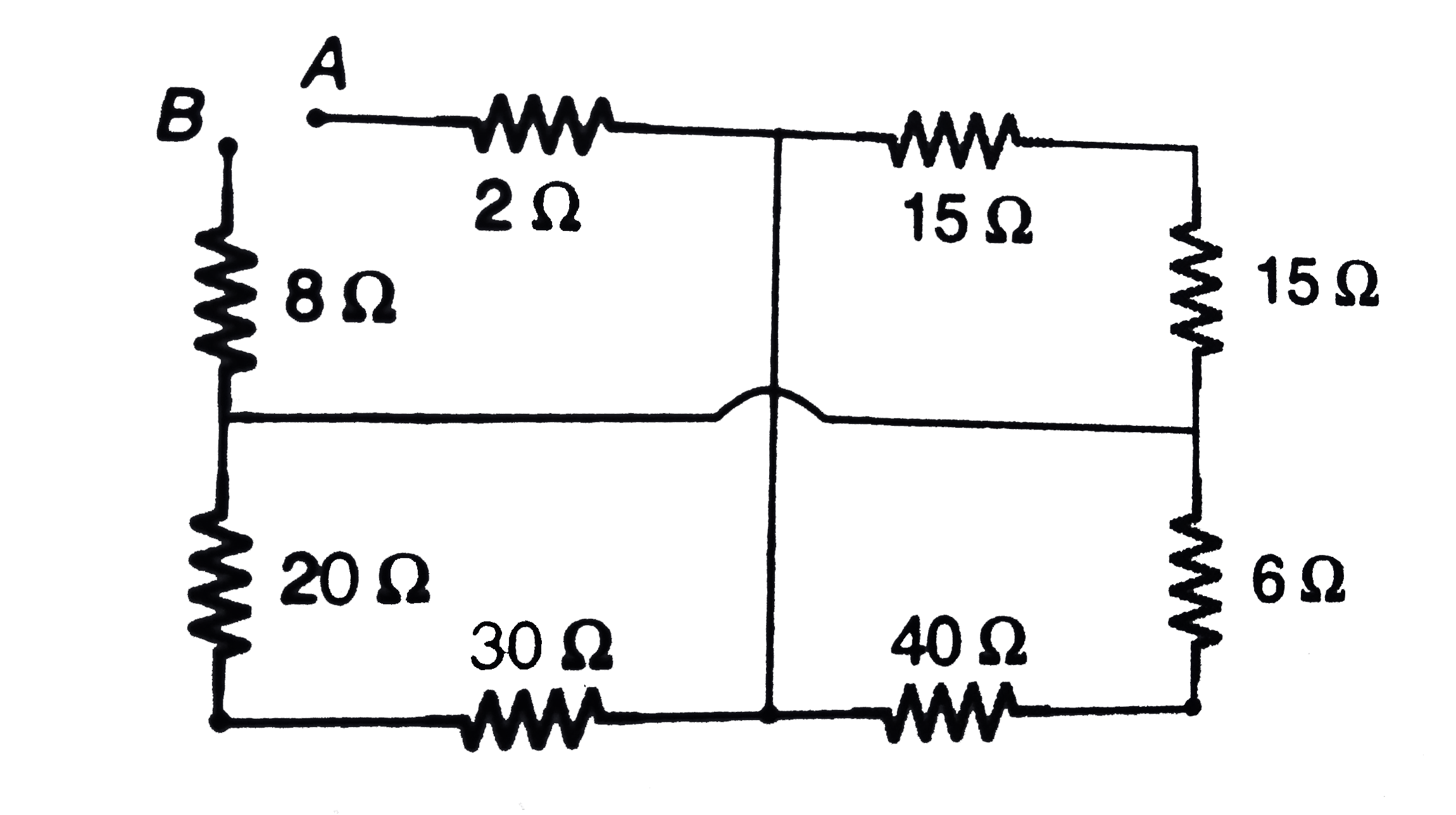 View Solution
View Solution

