Foot of a 10 m long ladder leaning against a verticle wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
To solve the problem, we will use the Pythagorean theorem, which relates the lengths of the sides of a right triangle.
1. Identify the components of the triangle:
- Let the length of the ladder be AB=10 m (hypotenuse).
- Let the distance from the wall to the foot of the ladder be BC=6 m (base).
- Let the height at which the ladder touches the wall be AC=h (perpendicular).
2. Set up the Pythagorean theorem:
According to the Pythagorean theorem:
AB2=AC2+BC2
Here, AB is the hypotenuse, AC is the height (perpendicular), and BC is the base.
3. Substitute the known values into the equation:
102=h2+62
This simplifies to:
100=h2+36
4. Rearrange the equation to solve for h2:
h2=100−36
h2=64
5. Take the square root of both sides to find h:
h=√64
h=8
6. Conclusion:
The height of the point on the wall where the top of the ladder reaches is 8 meters.
- Let the length of the ladder be AB=10 m (hypotenuse).
- Let the distance from the wall to the foot of the ladder be BC=6 m (base).
- Let the height at which the ladder touches the wall be AC=h (perpendicular).
According to the Pythagorean theorem:
AB2=AC2+BC2
Here, AB is the hypotenuse, AC is the height (perpendicular), and BC is the base.
102=h2+62
This simplifies to:
100=h2+36
h2=100−36
h2=64
h=√64
h=8
The height of the point on the wall where the top of the ladder reaches is 8 meters.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions18videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
A 6.5 m long ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall. Find the height of the wall where the top of the ladder touches it
View SolutionA ladder 3.7 m long is placed against a wall in such a way that the foot of the ladder is 1.2 m away from the wall. Find the height of the wall to which the ladder reaches.
View Solution
Knowledge Check
- Question 1 - Select One
A foot of a ladder leaning against the wall of a house is 4 feet from the base of the wall. If the ladder makes a 30∘ angle with the wall, what is the length, in feet, of the ladder ?
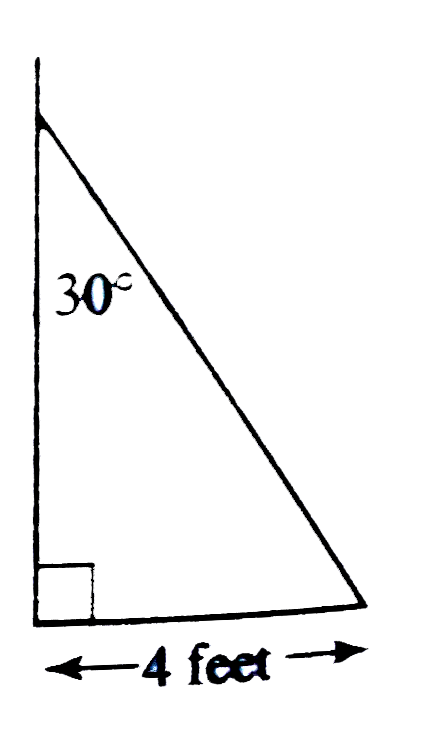 A2√3B4√3C8√3D8
A2√3B4√3C8√3D8 - Question 2 - Select One
A 10 m long ladder is placed against a wall in such a way that the foot of the ladder is 6 m away from the wall. Up to what height does the ladder reach the wall ?
A5mB6mC8mD9m - Question 3 - Select One
A 3m along ladder weighing 20kg leans on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the rection forces of the wall and the floor.
A25√2 N, 203 NB50√2 N, 230 NC203 N, 25√2 ND230N,50√2 N
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
View SolutionA ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
View SolutionA ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
View SolutionThe angle of elevation of a ladder leaning against a wall is 60∘ and the foot of the ladder is 9.5m away from the wall. Find the length of the ladder.
View SolutionA 3m along ladder weighing 20kg leans on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the rection forces of the wall and the floor.
View Solution

