AC Circuits
Step-by-Step Solution for AC Circuits
1. Understanding the AC Circuit:
- An AC circuit consists of alternating current and voltage, typically represented as:
V(t)=V0sin(ωt+ϕ)
- Here, V0 is the peak voltage, ω is the angular frequency, and ϕ is the phase angle.
Hint: Remember that the sine function indicates the periodic nature of AC signals.
2. Components of the AC Circuit:
- The main components in an AC circuit are:
- Resistor (R)
- Capacitor (C)
- Inductor (L)
- Together, they form an RLC circuit.
Hint: Identify each component's role in the circuit: resistors dissipate energy, capacitors store energy, and inductors store energy in a magnetic field.
3. Impedance in AC Circuits:
- Instead of resistance, we use impedance (Z) to analyze AC circuits.
- The impedance of each component is given as:
- Resistor: ZR=R
- Capacitor: ZC=−jωC (where j is the imaginary unit)
- Inductor: ZL=jωL
Hint: Recall that impedance combines both resistance and reactance, where reactance can be either positive (inductive) or negative (capacitive).
4. Total Impedance Calculation:
- The total impedance Z of the RLC circuit can be expressed as:
Z=R+j(ωL−1ωC)
- Here, R is the real part, and (ωL−1ωC) is the imaginary part.
Hint: Understand that the total impedance is a complex number, combining real and imaginary parts.
5. Magnitude of Impedance:
- The magnitude of the impedance |Z| is calculated using:
|Z|=√R2+(ωL−1ωC)2
Hint: This formula is similar to the Pythagorean theorem, where R is the adjacent side and the reactance is the opposite side.
6. Current in the Circuit:
- The current I in the circuit can be calculated using Ohm's law for AC circuits:
I=V|Z|
- If the voltage is expressed as V(t)=V0sin(ωt+ϕ), then:
I(t)=V0sin(ωt+ϕ)|Z|
Hint: Remember that the current lags or leads the voltage depending on the circuit's reactance.
7. Power Factor:
- The power factor (PF) is defined as:
PF=cos(ϕ)
- Where ϕ is the phase angle between the voltage and the current.
Hint: The power factor indicates how effectively the circuit converts electric power into useful work.
Summary
In an AC circuit with resistors, capacitors, and inductors, we analyze the circuit using impedance instead of resistance. The total impedance combines real and imaginary components, and we can calculate the current and power factor to understand the circuit's behavior.
- An AC circuit consists of alternating current and voltage, typically represented as:
V(t)=V0sin(ωt+ϕ)
- Here, V0 is the peak voltage, ω is the angular frequency, and ϕ is the phase angle.
- The main components in an AC circuit are:
- Resistor (R)
- Capacitor (C)
- Inductor (L)
- Together, they form an RLC circuit.
- Instead of resistance, we use impedance (Z) to analyze AC circuits.
- The impedance of each component is given as:
- Resistor: ZR=R
- Capacitor: ZC=−jωC (where j is the imaginary unit)
- Inductor: ZL=jωL
- The total impedance Z of the RLC circuit can be expressed as:
Z=R+j(ωL−1ωC)
- Here, R is the real part, and (ωL−1ωC) is the imaginary part.
- The magnitude of the impedance |Z| is calculated using:
|Z|=√R2+(ωL−1ωC)2
- The current I in the circuit can be calculated using Ohm's law for AC circuits:
I=V|Z|
- If the voltage is expressed as V(t)=V0sin(ωt+ϕ), then:
I(t)=V0sin(ωt+ϕ)|Z|
- The power factor (PF) is defined as:
PF=cos(ϕ)
- Where ϕ is the phase angle between the voltage and the current.
In an AC circuit with resistors, capacitors, and inductors, we analyze the circuit using impedance instead of resistance. The total impedance combines real and imaginary components, and we can calculate the current and power factor to understand the circuit's behavior.
Topper's Solved these Questions
Similar Questions
In the given AC circuit
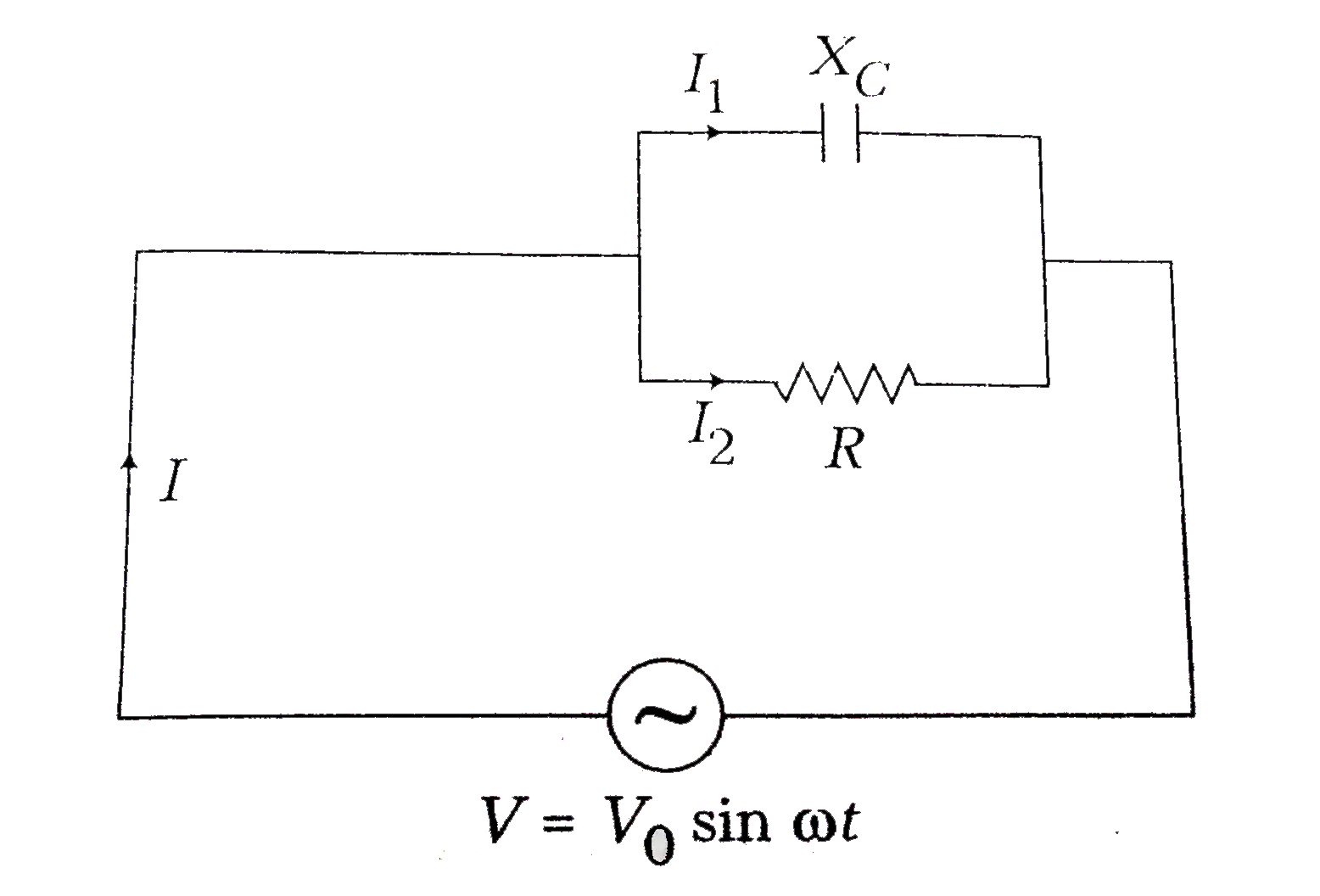
View SolutionIn a purely resistive AC circuit,
View SolutionIn an AC circuit, the power factor
View SolutionIn an AC circuit, the power factor
View SolutionThe term cosϕ in an AC circuit is called
View SolutionPhasor diagram of a series AC circuit is shown in figureure. Then,
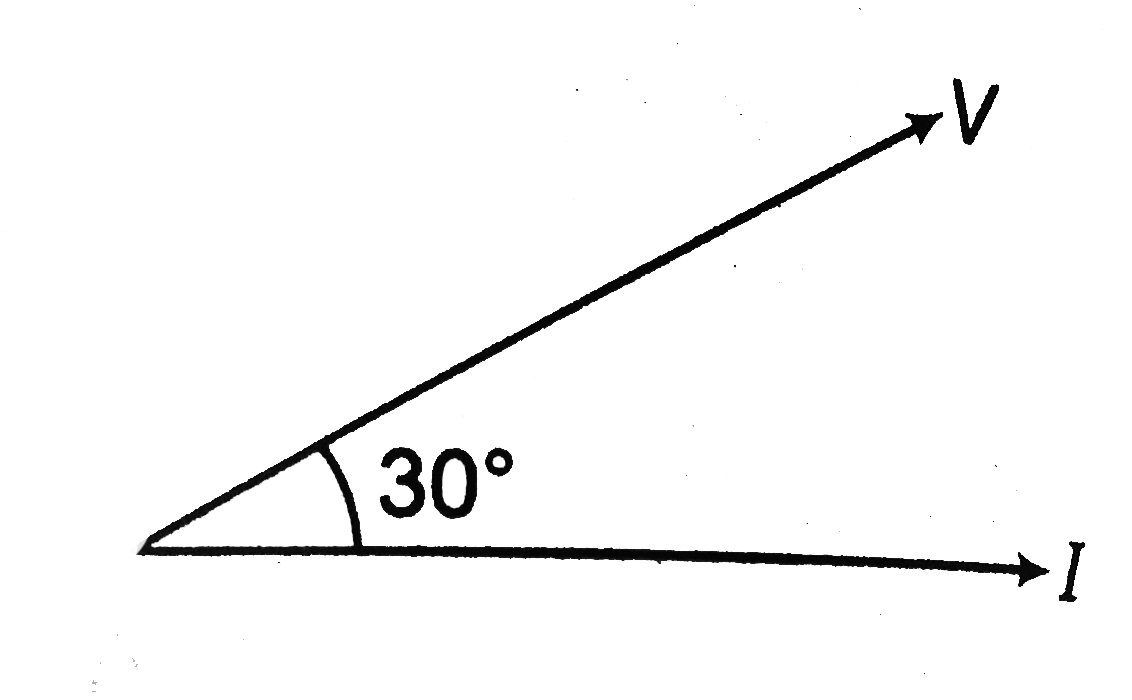
View SolutionIn an AC circuit containing only capacitance the current
View SolutionA choke coil is preferred to a rheostate in AC circuit as
View SolutionIn a series AC circuit containing a capacitor and a resistor only
View SolutionWhich of the following statement is incorrect about AC circuit?
View Solution
