The area bounded by the curves y=x(x−3)2andy=x is________ (in sq. units)
Video Solution
Text Solution
The correct Answer is:8
Required area =2∫20(x(x−3)2−x)dx=8 sq. units
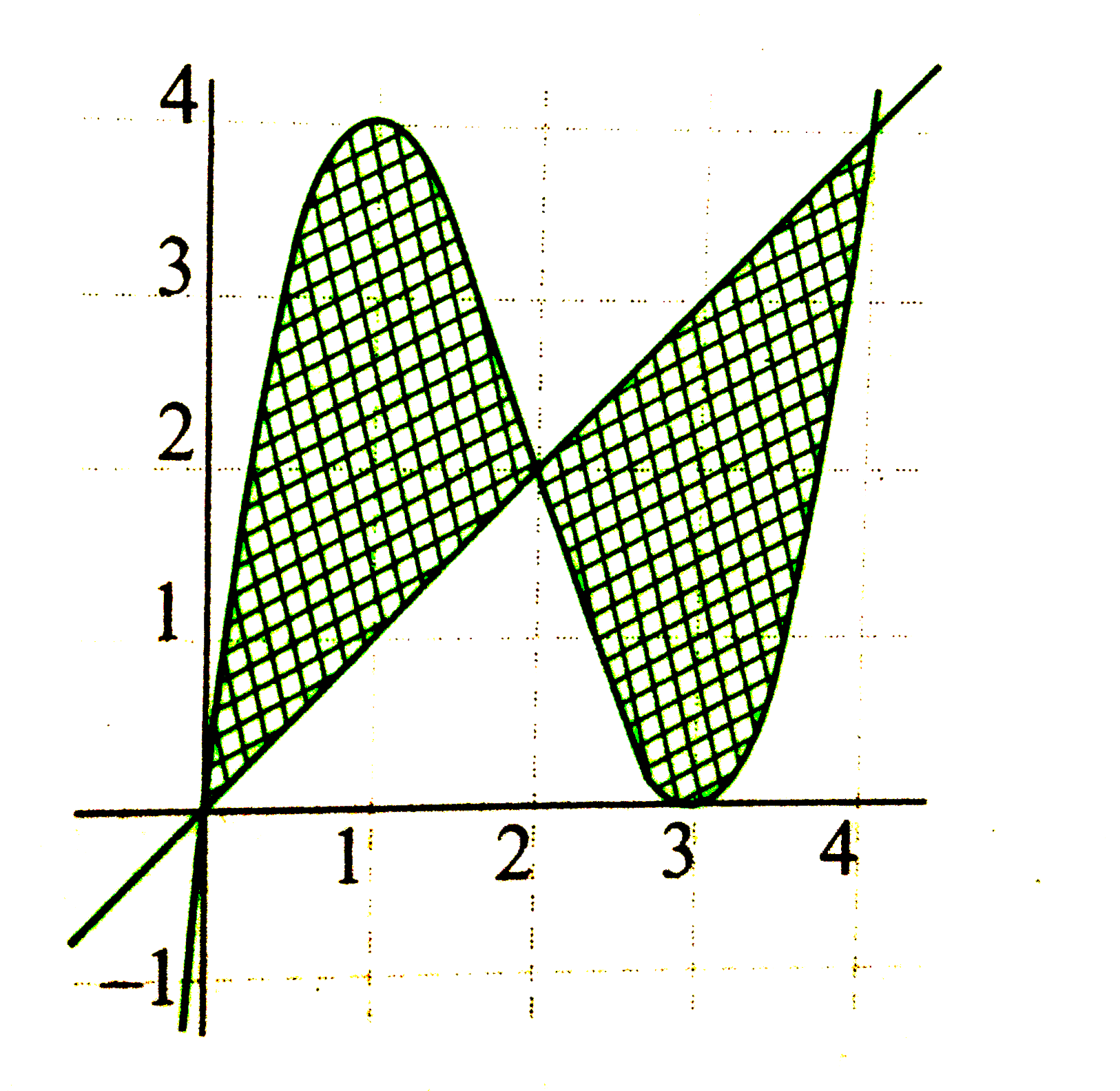
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives10videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type30videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
The area bounded by the curves y=x,y=x3 is
View SolutionFind the area bounded by the curves y=xandy=x3.
View SolutionArea bounded by the curves y=x2−1andx+y=3 is:
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area bounded by the curve y=3|x|andy+|2−x|=2 is
View SolutionThe area bounded between curves y2=xandy=|x|
View SolutionFind the area bounded by the curves y=6x−x2andy=x2−2x.
View SolutionThe area bounded by the curve y=4x−x2 and the x-axis is:
View SolutionThe area bounded by the curve y=4x−x2 and x-axis is (A) 307 sq. units (B) 317 sq. units (C) 323 sq. units (D) 343 sq. units
View Solution

