A farmer F1 has a land in the shape of a triangle with vertices at P(0, 0), Q(1, 1) and R(2, 0) . From this land, a neighbouring farmer F2 takes away the region which lies between the side PQ and a curve of the form y=xn (n>1) . If the area of the region taken away by the farmer F2 is exactly 30% of the area of PQR , then the value of n is _______.
The correct Answer is:4
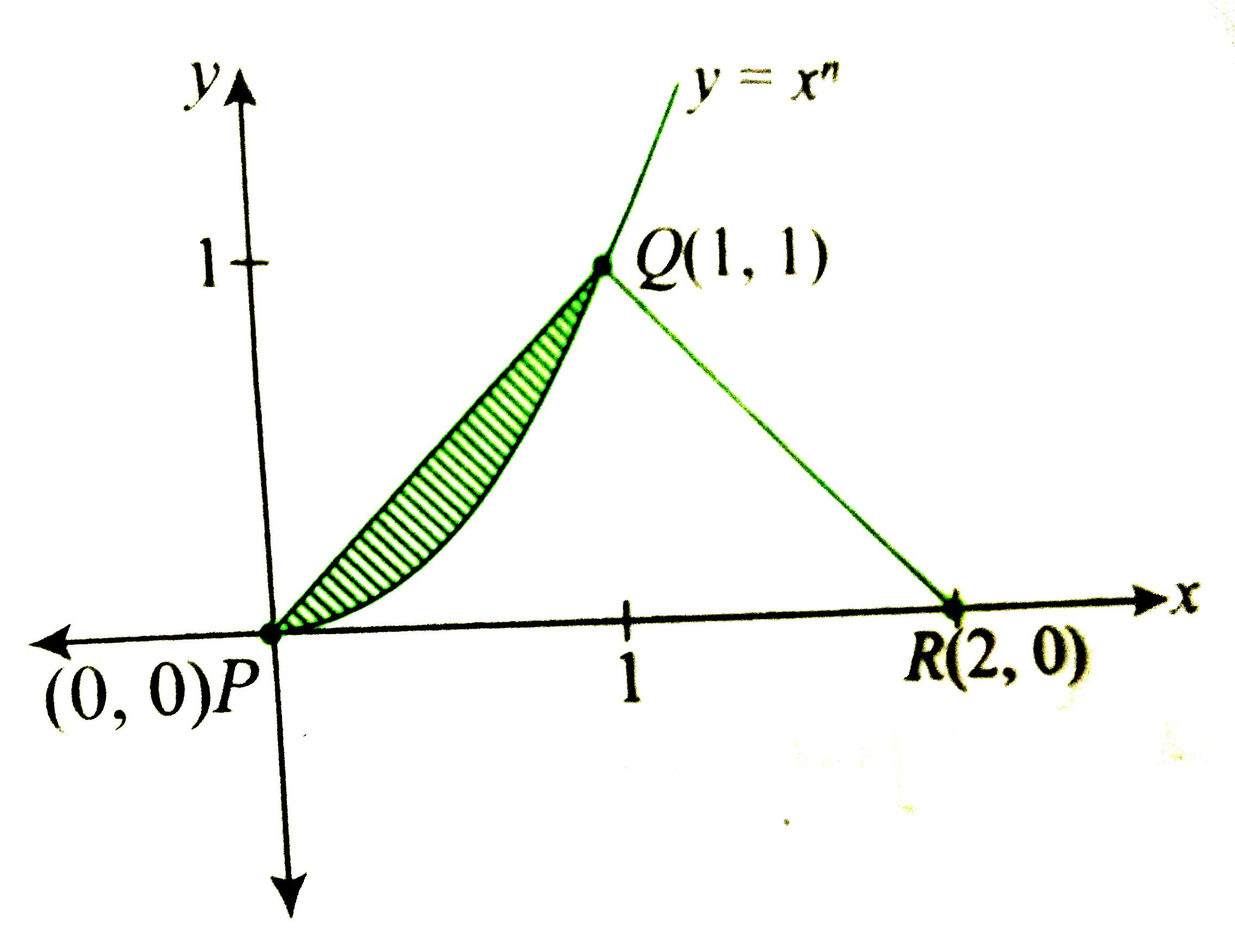
According to the question,
1∫0(x−xn)dx=310(12×2×1)
⇒ ∣∣∣x22−xn+1n+1∣∣∣10=310
⇒ 12−1n+1=310
⇒ 1n+1=12−310=15
⇒ n=4
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives10videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type30videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Knowledge Check
- Question 1 - Select One
If the lines p(p2+1)x−y+q=0 and (p2+1)2x+(p2+1)y+2q=0 are perpendicular to the same line, then the value of p is
A(a) 1B(b) −1C(c) 2D(d) −2
The point Q is the image of the P in line x+y+4=0 and R is the image of Q in line 2x−y+7=0. If P=(1,6), then the circumcentre of triangle PQR is
View SolutionTangent lines are drawn at the points P and Q where f''(x) vanishes for the function f(x)=cos x on [0,2π] The tangent lines at P and Q intersect each other at R so as to form a triangle PQR. If area triangle PQR is kπ2 then find the value of 36k.
View SolutionTangent lines are drawn at the points P and Q where f''(x) vanishes for the function f(x)=cos x on [0,2π] The tangent lines at P and Q intersect each other at R so as to form a triangle PQR. If area triangle PQR is kπ2 then find the value of 36k.
View SolutionP(2,1) , Q (4,-1) , R (3,2) are the vertices of a triangle and if through P and R lines parallel to opposite sides are drawn to intersect in S , then the area of PQRS , is
View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.View SolutionConsider a triangle PQR with P≡(0,0),Q≡(a,0),R≡(0,b). Then the centroid, orthocentre and circumcentre (A) lies on a straight line (B) form a scalene triangle with area a2|ab| (C) form a right-angled triangle with area 12|ab| (D) none of these
View SolutionLet F1(x1,0) and F2(x2,0), for x1<0 andx2>0, be the foci of the ellipse x29+y28=1. Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of the area of the triangle MQR to area of the quadrilateral MF1NF2 is :View Solution

