If the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2} is A , then the value of 3A−17 is____
The correct Answer is:6
Draw the given region point of intersection of y=x2+1
y=x+1
x+1=x2+1
x=0,1
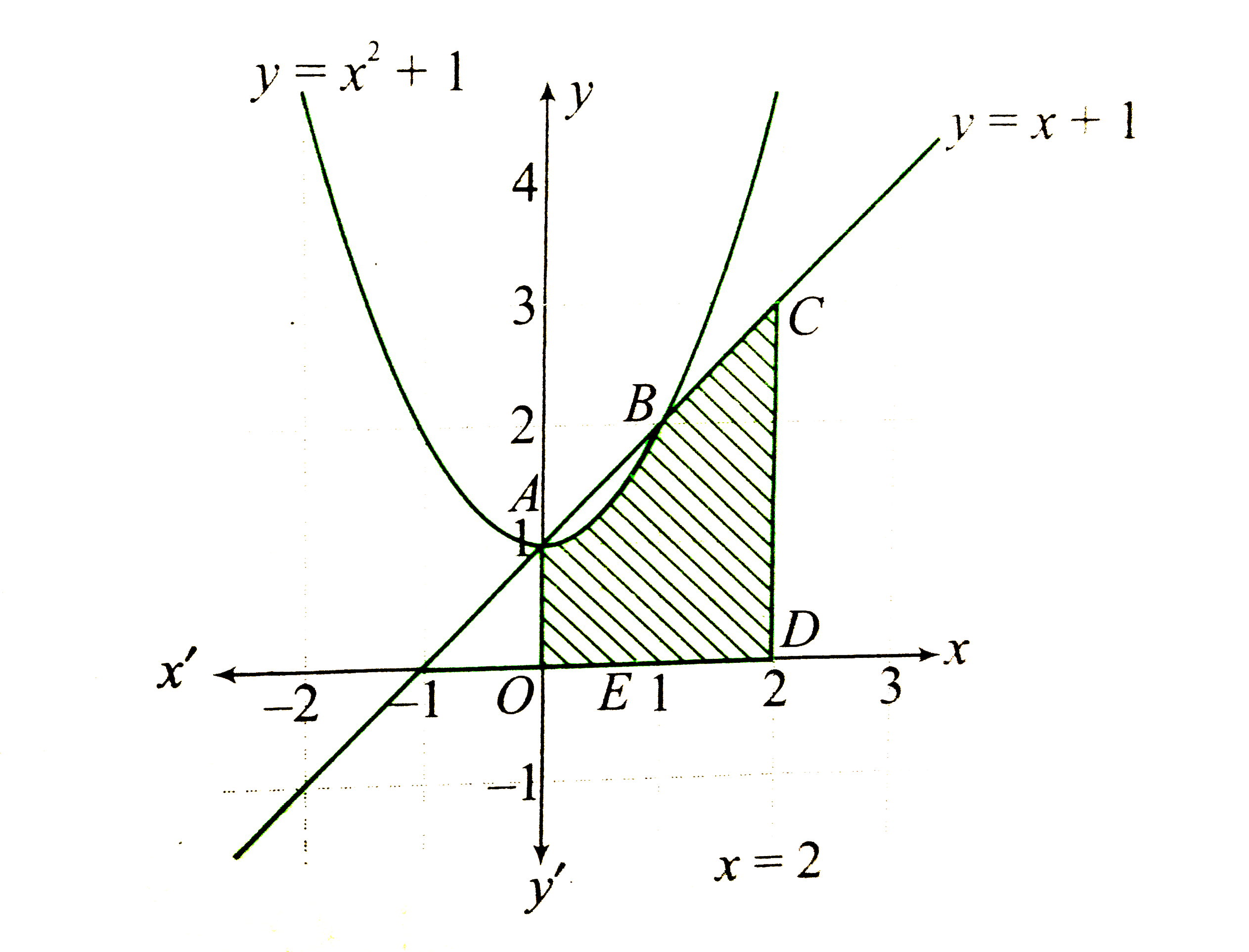
Required area OABCDE=1∫0(x2+1)dx+2∫1(x+1)dx
=(x33+x)10+(x22+x)21=236 sq. units
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives10videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type30videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Find the area of the region {(x,y):x2≤y≤|x|}.
View SolutionFind the area of the region {(x,y):x2+y2≤1≤x+y}.
View SolutionIf the area (in sq. units) of the region
{(x,y):y2≤4x,x+y≤1,x≥0,y≥0} is a√2+b, then a−b is equal to :View SolutionIf m is the minimum value of f(x,y)=x2−4x+y2+6y when xandy are subjected to the restrictions 0≤x≤1and0≤y≤1, then the value of |m| is________
View SolutionIf m is the minimum value of f(x,y)=x2−4x+y2+6y when xandy are subjected to the restrictions 0≤x≤1and0≤y≤1, then the value of |m| is________
View SolutionThe area of the region described by A={(x,y):x2+y2≤1andy2≤1−x} is
View Solutionthe area of region for which 0<y<3−2x−x2 and x>0 is
View SolutionVerify Rolles theorem for the function f(x)=x(x−3)2, 0≤x≤3 .
View SolutionIf [] denotes the greatest integer less than or equal to the real number under consideration and −1≤x<0,0≤y<1,1≤z<2, the value of the determinant ∣∣ ∣ ∣∣[x]+1[y][z][x][y]+1[z][x][y][z]+1∣∣ ∣ ∣∣ is
View SolutionFind the maxima and minima of the function y=x(x−1)2,0≤x≤2.
View Solution

