Question

For a point $P$
in the plane, let $d_1\left(P\right)and{d}_2\left(P\right)$
be the distances of the point $P$
from the lines $x-y=0andx+y=0$
respectively. The area of the region $R$
consisting of all points $P$
lying in the first quadrant of the plane and satisfying $2\le d_1\left(P\right)+d_2\left(P\right)\le 4,$
is

Answer

6

Explanation

For P(x,y), we have
`2led_(1)(P)+d_(2)(P)le4`
`rArr" "2le(|x-y|)/(sqrt(2))+(|x+y|)/(sqrt(2))le4`
`rArr" "2sqrt(2)le |x-y|+|x+y|le4sqrt(2)`
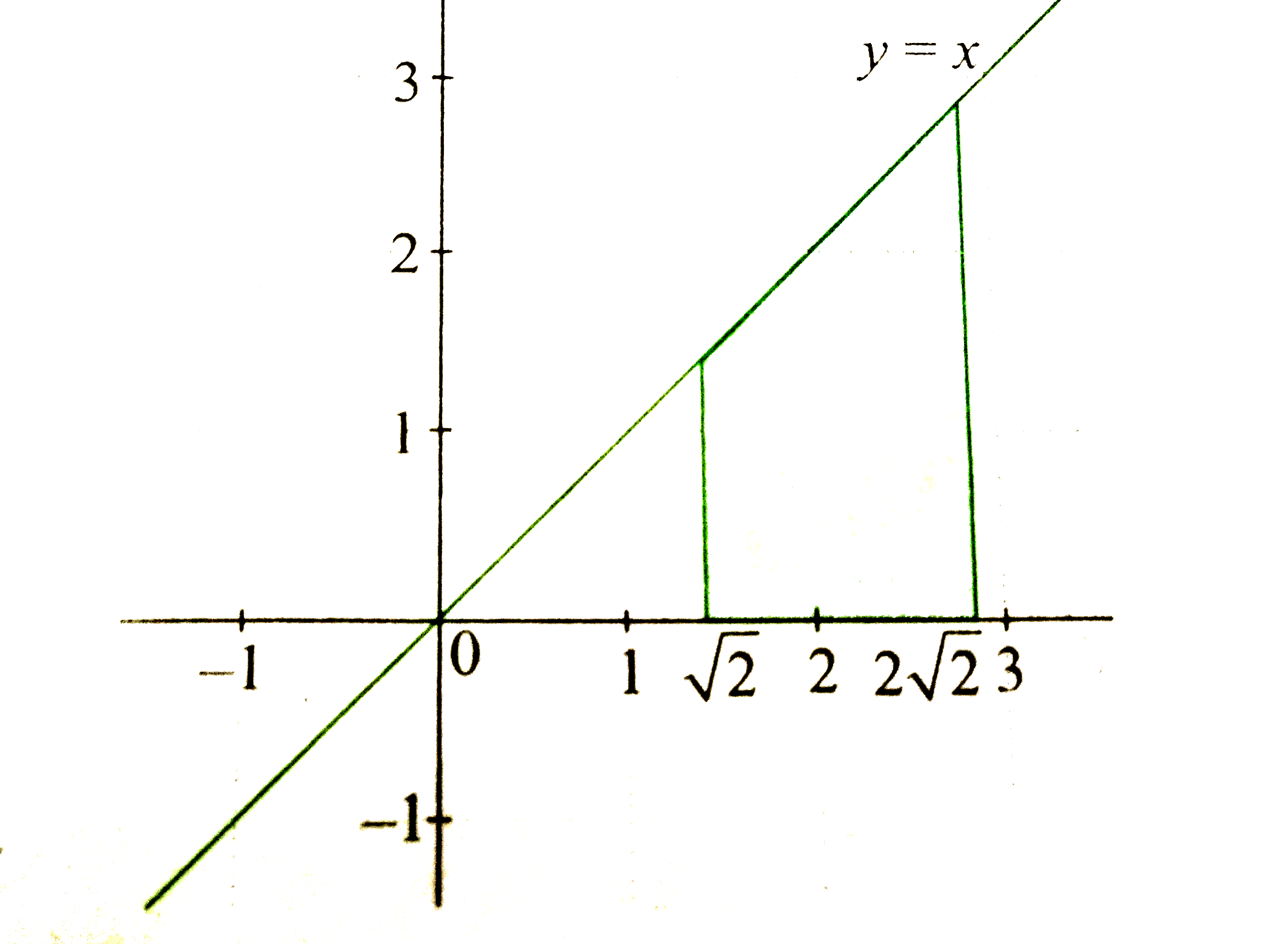
IN first quadrant if `xgty,` we have
`2sqrt(2)lex-y+x+yle4sqrt(2)`
`"or "sqrt(2)lexle2sqrt(2)`
The region of points satisfying these inequalities is

In first quadrant if `xlty`, we have
`2sqrt(2)ley-x+x+yle4sqrt(2)`
`"or "sqrt(2)leyle2sqrt(2)`
The region of points satisfying these inequalities is

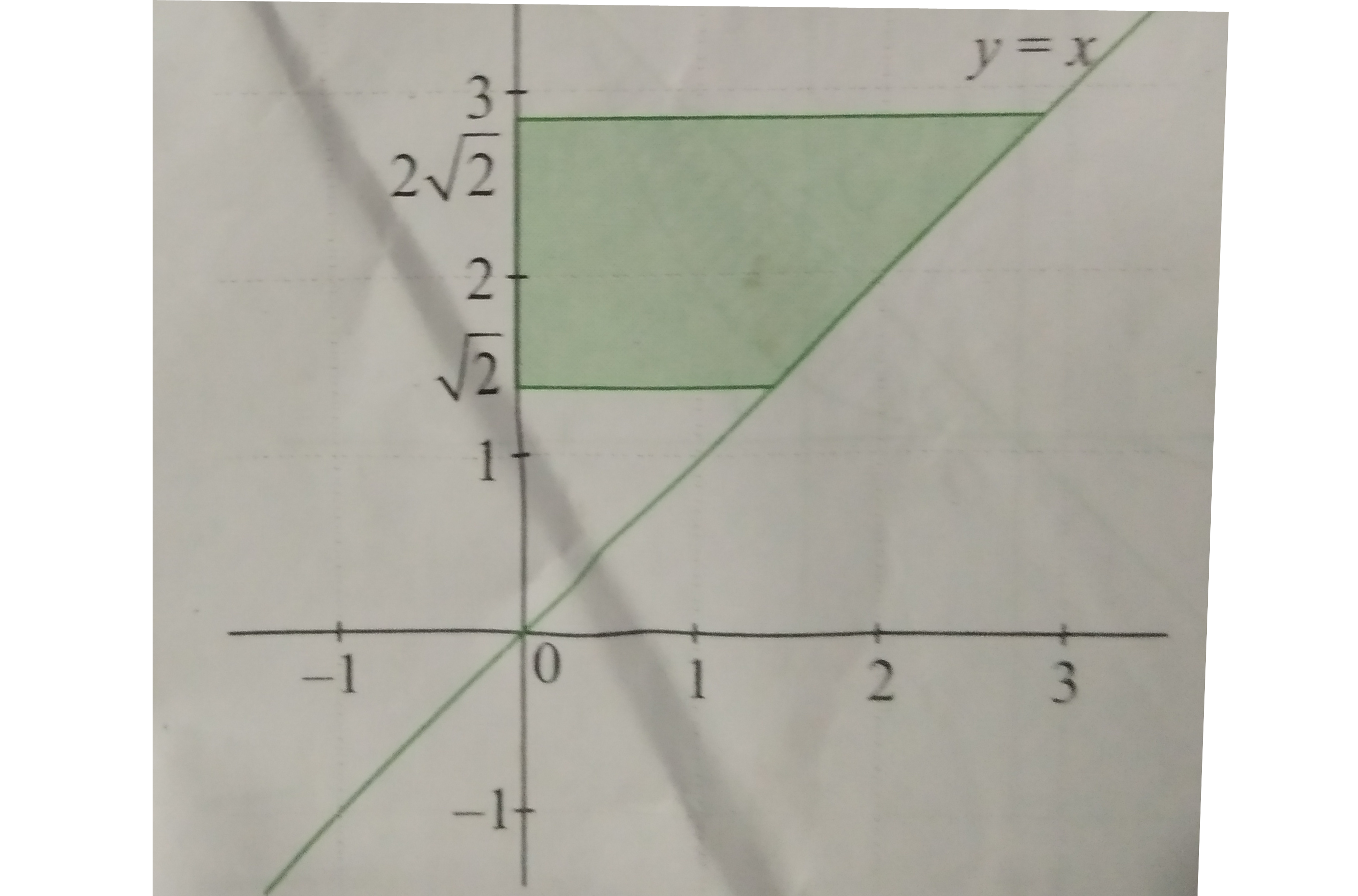
Combining above two regions we have

Area of the shaded region `=((2sqrt(2))^(2)-(sqrt(2))^(2))`
`=8-2=6` sq. units