Question

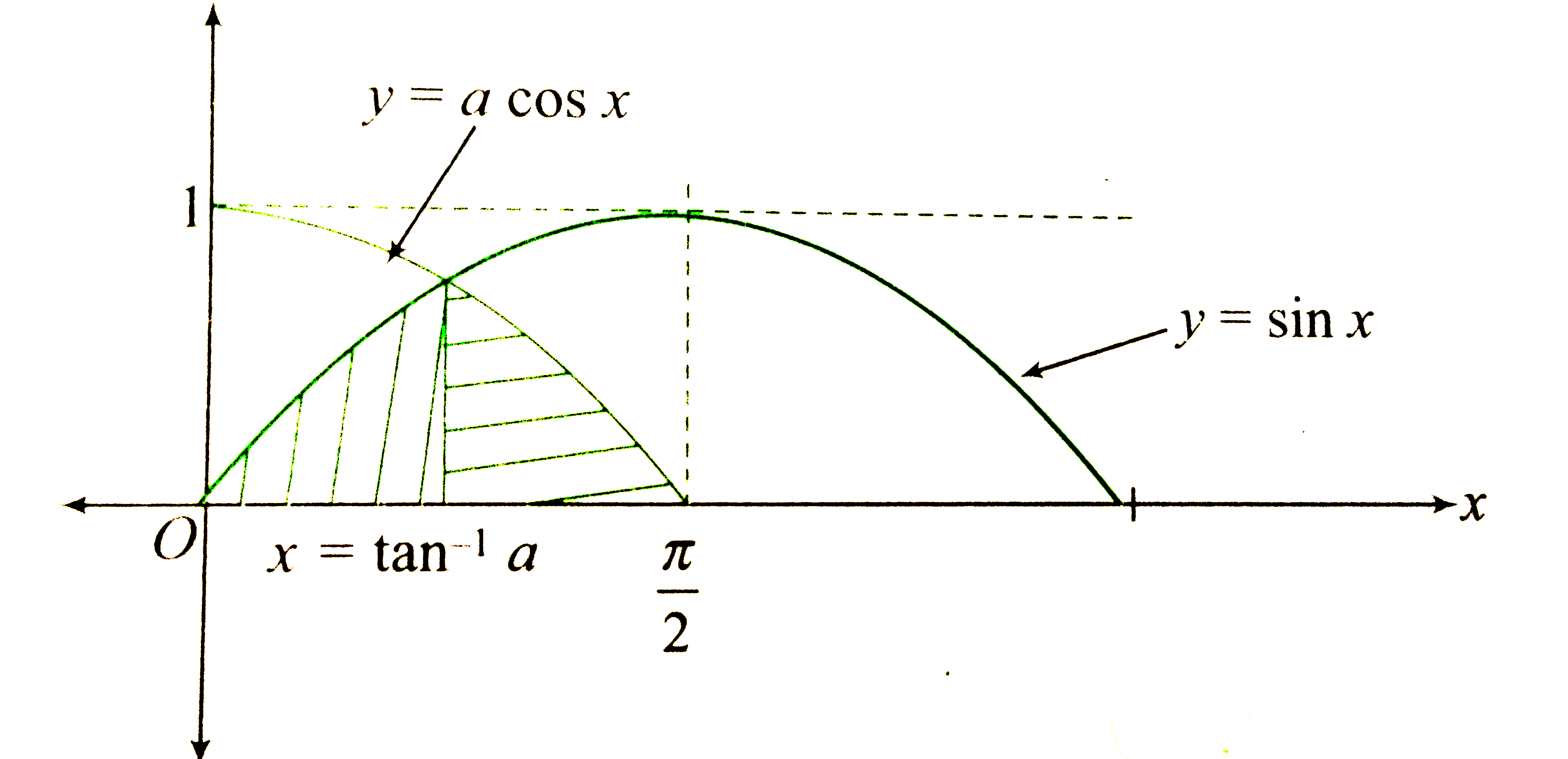
Let $S$
be the area bounded by the curve $y=\sin x(0\le x\le \pi )$
and the x-axis and $T$
be the area bounded by the curves
$y=\sin x(0\le x\le \frac{\pi }{2}),y=a\cos x(0\le x\le \frac{\pi }{2}),$
and the x-axis $(wherea\in R^{+})$

The value of $\left(3a\right)$
such that $S:T=1:\frac{1}{3}$
is______

Answer

4

Explanation

We have `S=overset(pi)underset(0)sin x dx =2, so T=(2)/(3)," where "agt0.`
`"Now "T=overset(tan^(-1)a)underset(0)intsin x dx +overset(pi//2)underset(tan^(-1)a)inta cos x dx =(2)/(3)`

`i.e., -cos (tan^(-1)a)+1+a{[1-sin (tan^(-1)a)]}=(2)/(3)`
`i.e., -(1)/(sqrt(1+x^(2)))+1+a-(a^(2))/(sqrt(1+a^(2)))=(2)/(3)`
`"or "(a+1)-sqrt(a^(2)+1)=(2)/(3)or a +(1)/(3)=sqrt(a^(2)+1)`
`"or "a=(4)/(3)`
`"Hence, "3a=4`.