Draw the graph of $y = \sin x \cos^{2} x$

Video Solution

Text Solution

Verified by Experts

We have $y = f (x) = \sin x \cos^{2} x$
Clearly, the domain of $f (x)$ is R.
Also the period of $f (x)$ is R.
Let us first draw the graph of $y = f (x)$ for $0 \leq x \leq 2 π$
$f (x) = 0 ∴ \sin x = 0$ or $\cos^{2} x = 0$
$∴ x = 0, π, 2 π$ or $x = π / 2, 3 π / 2$
$f (x) > 0$ , for $x \in (0, π)$ and $f (x) < 0$ , for $x \in (π, 2 π)$
Now $f^{'} (x) = \cos x \cos^{2} x + \sin x (- 2 \sin x \cos x)$
$= \cos x (\cos^{2} x - 2 \sin^{2} x)$
$f^{'} (x) = 0 ∴ \cos x = 0$ or $\tan^{2} x = 1 / 2$
$∴ x = \frac{π}{2}, \frac{3 π}{2}$ or $x = \frac{\tan^{- 1} 1}{\sqrt{2}}, π - \frac{\tan^{- 1} 1}{\sqrt{2}}, π + \frac{\tan^{- 1} 1}{\sqrt{2}}, 2 π - \frac{\tan^{- 1} 1}{\sqrt{2}}$
Now we can draw the graph of $y = f (x)$ for $x \in (0, π)$
For $x \in (π, 2 π)$ , we reflect the graph of $y = f (x)$ for $x \in (0, π)$ in the x-axis as $f (π - x) = - f (π + x)$
$f (\frac{\tan^{- 1} 1}{\sqrt{2}}) = f (π - \frac{\tan^{- 1} 1}{\sqrt{2}}) = \frac{2}{3 \sqrt{3}}$
From the above discussion, we have, following important points on graph paper.

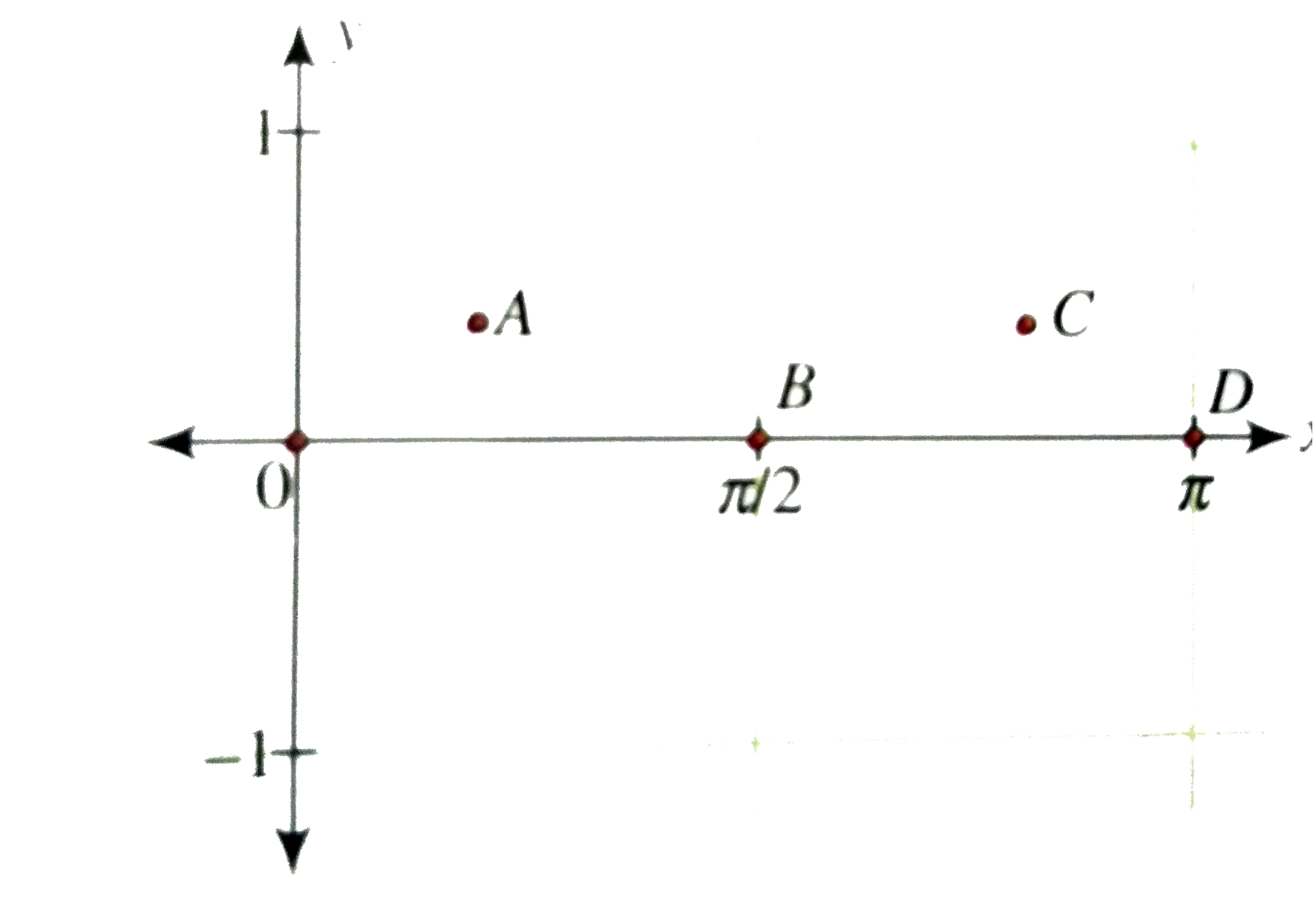
$f (x)$ increases from O to A, decreases from A to B, increases from B to C, decreases from C to D.
Hence the graph of $y = f (x)$ for $0 < x < π$ is as shown in the following figure.

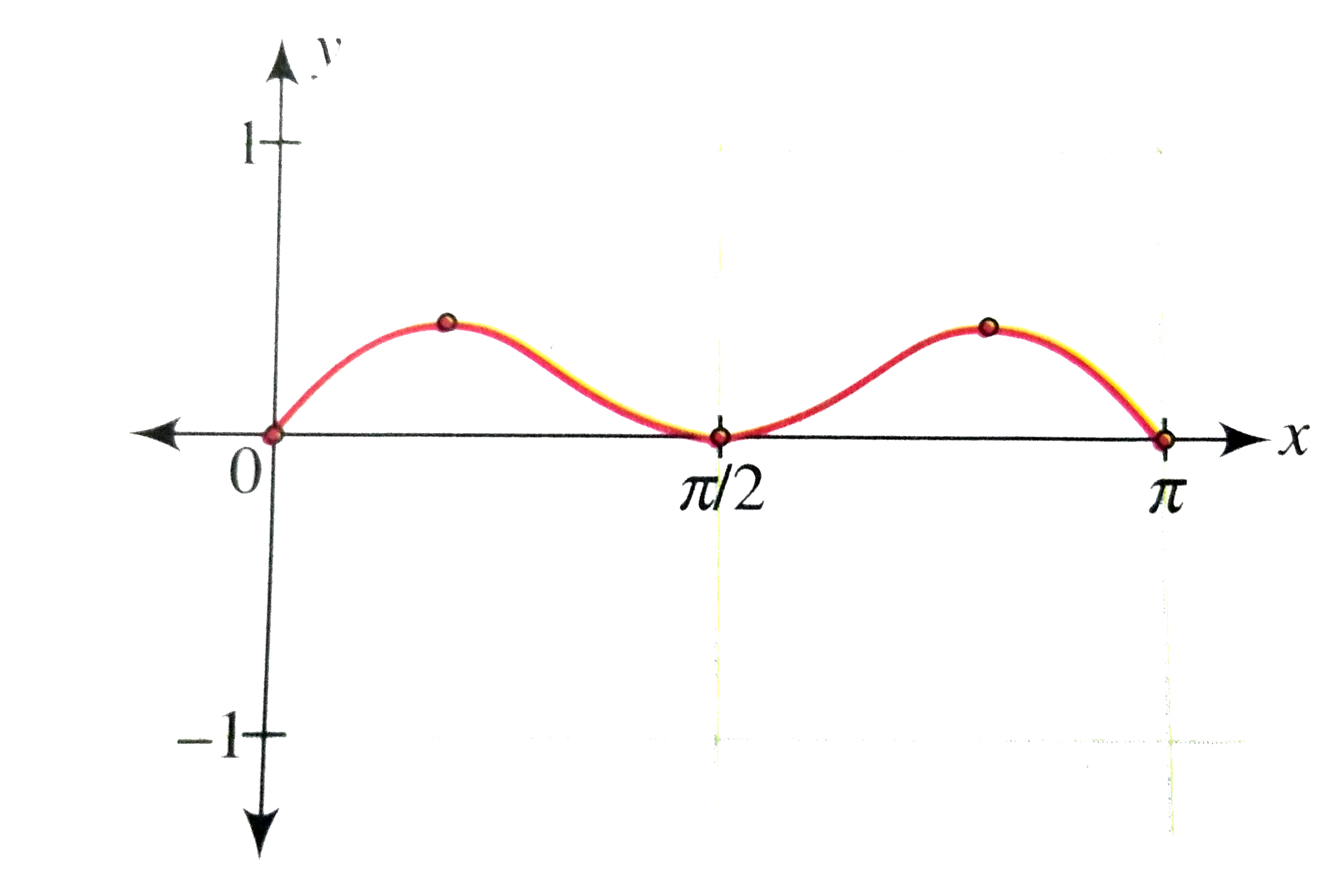
For $π < x < 2 π$ , the graph of $y = f (x)$ lies below the x-axis.
Hence, the graph of $y = f (x)$ for $π < x < 2 π$ is as shown in the following figure.

Since the period of $f (x)$ is $2 π$ , the graph for R is as follows:

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

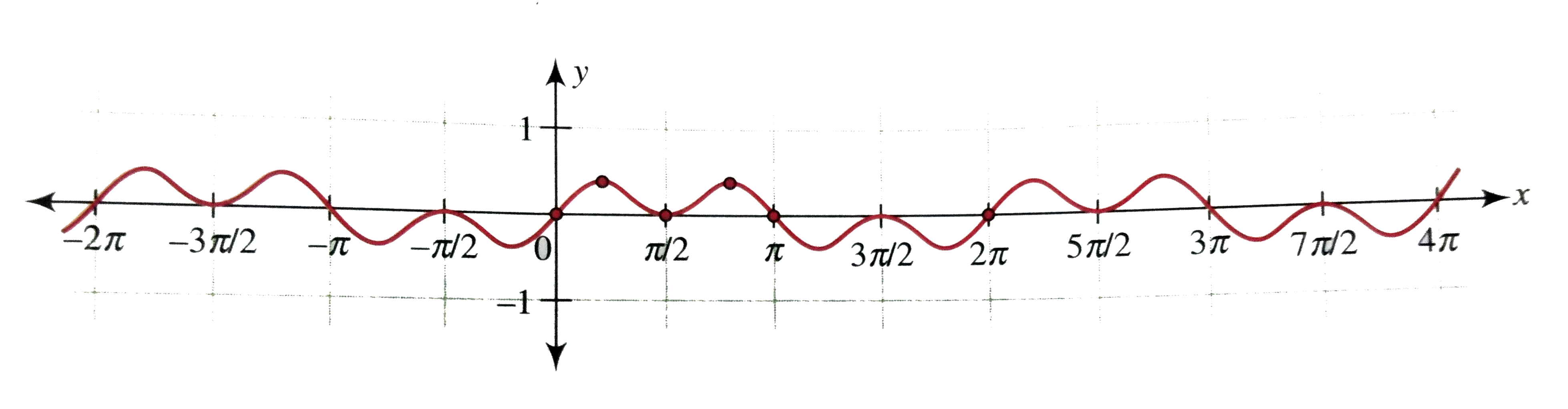
Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CURVE TRACING-EXERCISES

Home
Ask Doubt
Profile