Question

Draw the graph of y=$\frac{x^2}{\sqrt{x+1}}$

Explanation

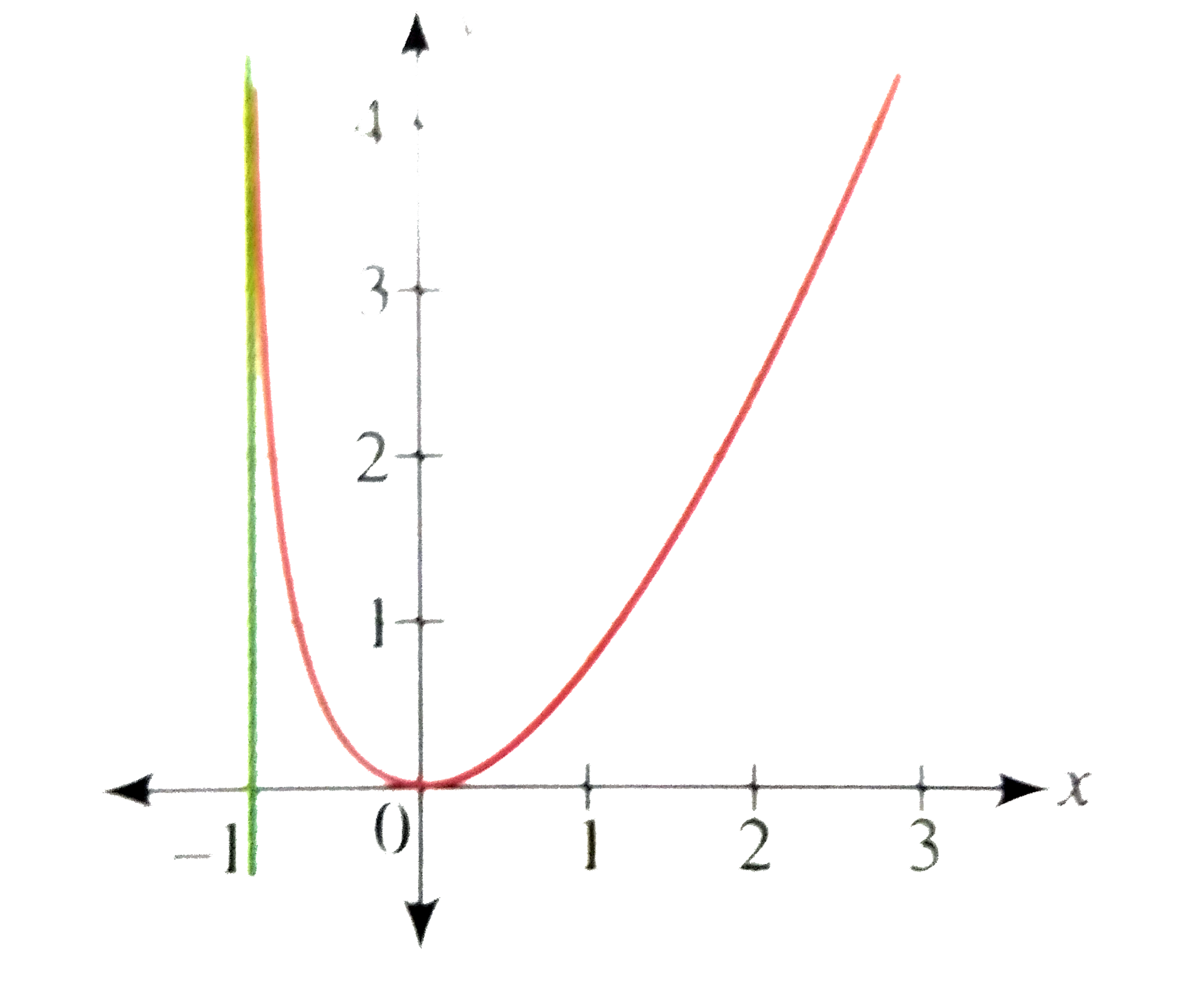
We have, `y=f(x) = x^(2)/sqrt(x+1)`
Clearly, the domain of the function is `(-1, infty)`.
`x^(2)/sqrt(x+1) ge0, AA x in (-1,infty)`
So the graph of `y=f(x)` lies entirely above the x-axis.
`underset(x to -1^(+))(x^(2))/sqrt(x+1)=infty`
`f(0)=0`
`f^(')(x) = 2xsqrt(x+1)-x^(2)/(2sqrt(x+1)) /(x+1)`
`=(4x(x+1)-x^(2))/(2(x+1)sqrt(x+1))`
`=(x(3x+4))/(2(x+1)sqrt(x+1))`
`f^(')(x) lt 0` for `-1 lt x lt 0`. Where `f(x)` decreases and `f^(')(x)` increases. Hence, `x=0` is point of minima.
`underset(x to infty)"lim"(x^(2)/sqrt(x+1))=infty`
Hence graph of functions is as shown in the following figure.