Draw the graph of f(x)=x2e−|x|
i) Find the point of maxima/minima.
ii) Find the asymptote is any.
iii) Find the range of the function.
iv) Find the number of roots of the equation f(x)=1
Video Solution
Text Solution
we have f(x)=x2e−|x|
Clearly, f(x)=f(−x).
So f(x) is an even function.
Hence the graph is symmetrical about the y-axis.
For x≥0,f(x)=x2e−x
Now f′(x)=−x2e−x+2xe−x=xe−x(2−x)
f′(x)=−x2e−x+2xe−x=xe−x(2−x)
f′(x)=0⇒x=0 or x=2
f(0)=0 and limx→∞x2ex=limx→∞2xex=2x→∞ex=0
So x=2 is the pont of maxima.
Hence the graph of f(x) is as shown in the following figure.
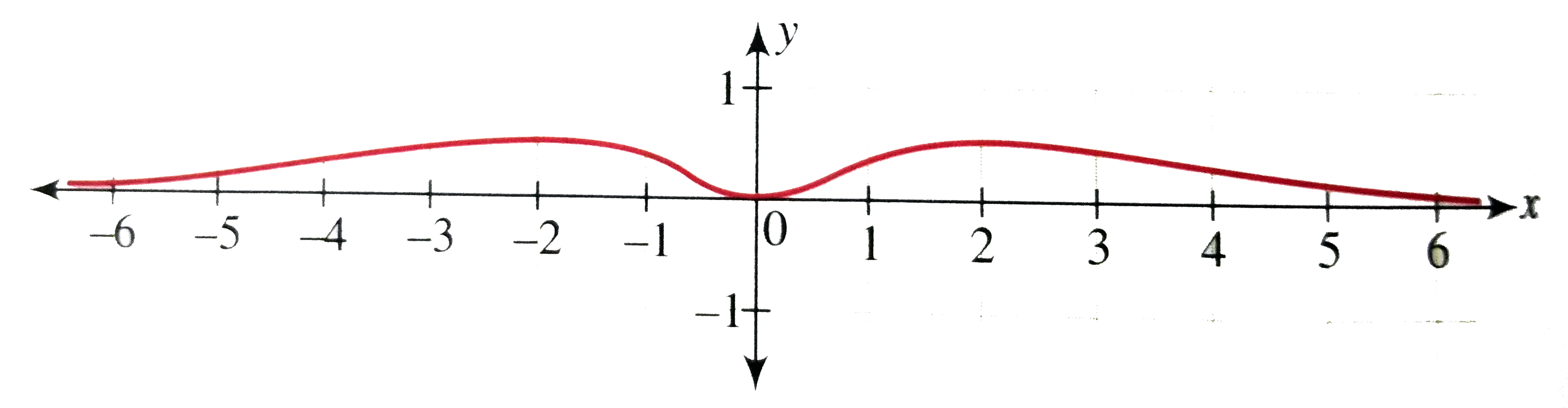
Since, f(x) is differentiable at x=0,the graph touches the x-axis at x=0
The x-axis is also asymptote to the curve.
Also since f(x) is an even function, x=−2 is also the point of maxima.
Range of the function is [0,f(2)] or [0,4/e2]
Clearly, f(x)≠1, hence f(x)=1 has no roots.
|
Topper's Solved these Questions
Similar Questions
Find the range of the function f(x) = -|x|.
View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
View SolutionFind the range of the function f(x)=x2−2x−4.
View SolutionDraw the graph of f(X)=loge(1−logex). Find the point of inflection
View SolutionDraw graph of f(x) =x|x−2| and hence find points of local maxima/minima.
View SolutionDraw the graph of f(x)=|x|−|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|2x−1|+|2x−3|. Find the range of the function.
View SolutionThe graph of the function y=f(x) is shown.

Find the number of solutions to the equation ||f(x)|−1|=12.
View SolutionDraw and graph of f(x)=4logexx2. Also find the range.
View Solution
