Discuss the number of roots of the equation e(k−xlogx)=1 for different value of k.
Video Solution
Text Solution
e(k−xlogx)=1
⇒k−1e=xlogx
Then Eq. (i) has solution where the graphs of y=xlogxand y=k−1e intersects. Now, consider the function f(x)=xlogex
f(x)=0∴x=1
f(x)>0 for x>1
f(x)<0 for 0<x<1
limx→0+(x.logex)(0×∞form)
=limx→0+1x−1x2=limx→0+(−x)=0
Now f′(x)=x.1x+logex=1+logex
f′(x)=0∴f''(1/e)=e>0, so x=1/e is the point of minima.
f(x) decreases in (0,1e) from 0 to −1e and increases in (1e,∞) from −1e to ∞, intersecting the x-axis at (1,0)
Hence the graph of f(x)=xlogex is as shown in the following figure.
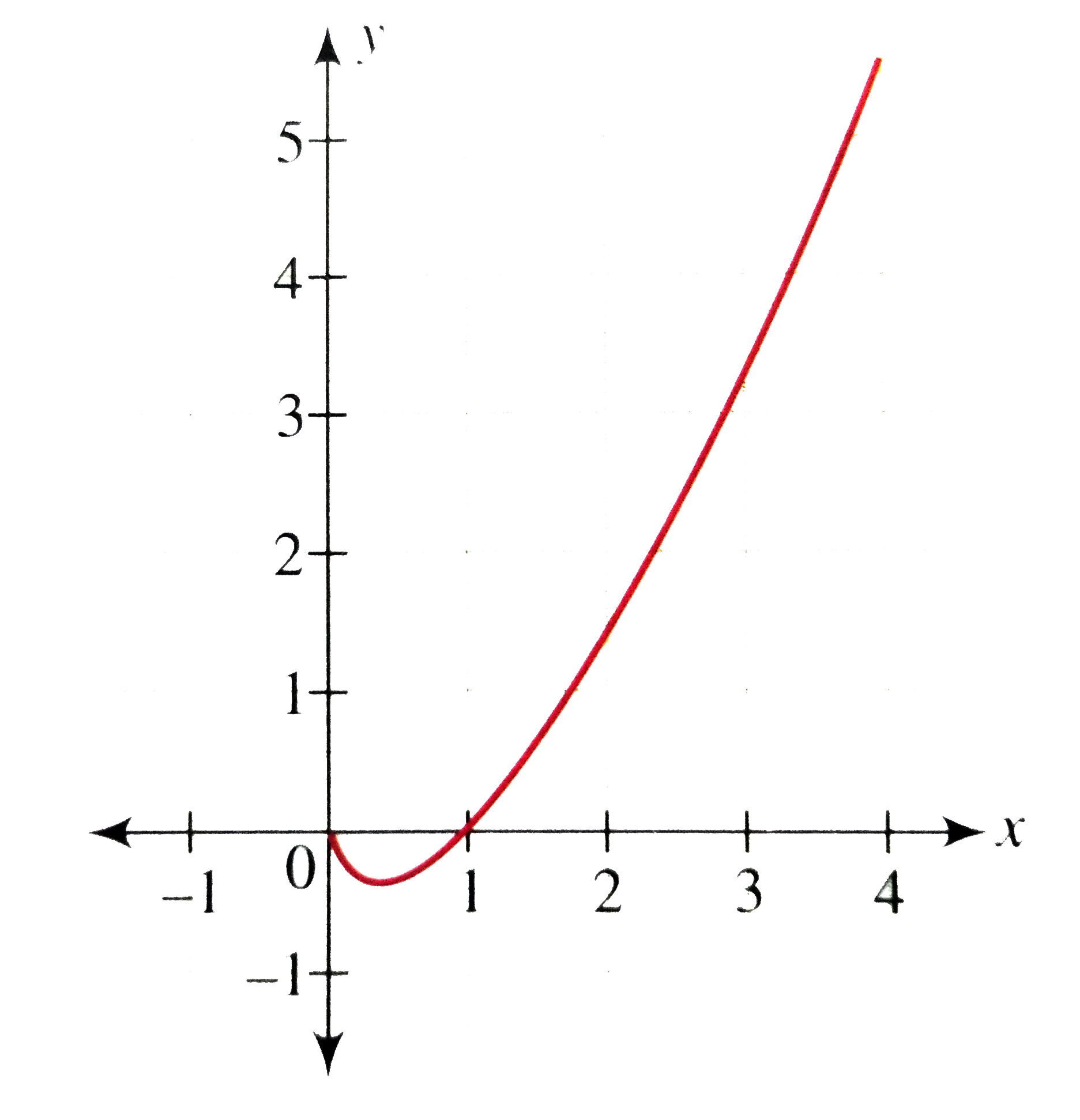
Hence, the graph of f(x)=xlogex is as shown in the following figure.
Hence the equation k−1e=xlogex has two distinct roots.
if −1e<k−1e<0⇒0<k<1e
The equation has no roots if k−1e<−1e⇒k<0
The equation has one root if k−1e=1e or k−1e≥0⇒=0 or k≥1e
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the roots of the equation x2+8x−(2k+3)=0 differ by 2, then the value of k is
A9B−9C6D−6
Find the number of roots of equation xsinx=1
View SolutionThe number of roots of the equation, x−2x−1 is
View SolutionNumber of real roots of the equation ex−1−x=0 is
View SolutionFind the number of roots of the equation ex=√−x.
View SolutionThe number of real root of the equation ex−1+x−2=0, is
View SolutionIf k<0, then the number of roots of the equation kex−x=0, is
View SolutionNumber of solutions of the equation e(k−xlnx)=1 for kε(0,1e) are:
View Solution
