In Figure, if PR is tangent to the circle at P and Q is the centre of the circle, then ∠POQ=
1100
1000
1200
900
The correct Answer is:C
To find the angle ∠POQ in the given scenario, we can follow these steps:
Step 1: Identify the Components
- We know that PR is a tangent to the circle at point P.
- Q is the center of the circle.
- OP and OQ are the radii of the circle.
Step 2: Establish Relationships
- Since OP and OQ are both radii of the circle, we have:
OP=OQ
- Therefore, triangle OPQ is isosceles, which means:
∠OPQ=∠OQP
Step 3: Use the Tangent Property
- The tangent at any point on a circle is perpendicular to the radius at that point. Therefore:
∠OPR=90∘
Step 4: Determine Remaining Angles
- We also know that ∠RPQ is given as 60∘.
- Thus, we can find ∠OPR and ∠RPQ:
∠OPQ=∠OQP=∠OPR−∠RPQ=90∘−60∘=30∘
Step 5: Apply the Triangle Sum Property
- The sum of angles in triangle OPQ is 180∘:
∠OPQ+∠OQP+∠POQ=180∘
- Substituting the known values:
30∘+30∘+∠POQ=180∘
Step 6: Solve for ∠POQ
- Simplifying the equation:
60∘+∠POQ=180∘
- Therefore:
∠POQ=180∘−60∘=120∘
Final Answer
Thus, the angle ∠POQ is 120∘.
---
- We know that PR is a tangent to the circle at point P.
- Q is the center of the circle.
- OP and OQ are the radii of the circle.
- Since OP and OQ are both radii of the circle, we have:
OP=OQ
- Therefore, triangle OPQ is isosceles, which means:
∠OPQ=∠OQP
- The tangent at any point on a circle is perpendicular to the radius at that point. Therefore:
∠OPR=90∘
- We also know that ∠RPQ is given as 60∘.
- Thus, we can find ∠OPR and ∠RPQ:
∠OPQ=∠OQP=∠OPR−∠RPQ=90∘−60∘=30∘
- The sum of angles in triangle OPQ is 180∘:
∠OPQ+∠OQP+∠POQ=180∘
- Substituting the known values:
30∘+30∘+∠POQ=180∘
- Simplifying the equation:
60∘+∠POQ=180∘
- Therefore:
∠POQ=180∘−60∘=120∘
Thus, the angle ∠POQ is 120∘.
Topper's Solved these Questions
Similar Questions
In Figure, if PR is tangent to the circle at P and Q is the centre of the circle, then ∠POQ=
View SolutionIf PT is tangent drawn from a point P to a circle touching it at T and O is the centre of the circle, then ∠OPT+∠POT= (a)30∘ (b)60∘ (c)90∘ (d)180∘
View SolutionIn Figure, find m ∠PQB where O is the centre of the circle
View SolutionPQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR=120o , then ∠OPQ is 60o (b) 45o (c) 30o (d) 90o
View SolutionIn Fig. 10.62, PO⊥QO . The tangents to the circle at P and Q intersect at a point T . Prove that PQ and OT are right bisectors of each other. (FIGURE)
View SolutionDraw a circle with centre O and radius 6 cm . Mark points P, Q, R such that P lies on the circle, Q lies in the interior of the circle , and R lies in the exterior of the circle. Rewrite each of the following statements using the correct symbol (=, ⟨or⟩): (i) OQ5 cm (ii) OP.5cm (iii) OR.5 cm
View SolutionIn the following figure, the line ABCD is perpendicular to PQ, where P and Q are the centres of the circles. Show that :
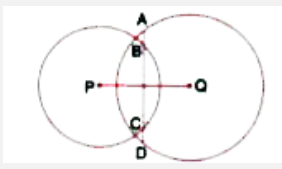
AC=BD
View SolutionIn Figure, APB is a tangent to a circle with centre O at point P . If ∠QPB=50∘ , then the measure of ∠POQ is (a)100∘ (b) 120∘ (c) 140∘ (d) 150∘
View SolutionCircles with centres P and Q intersects at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent, show that : CE = BD.
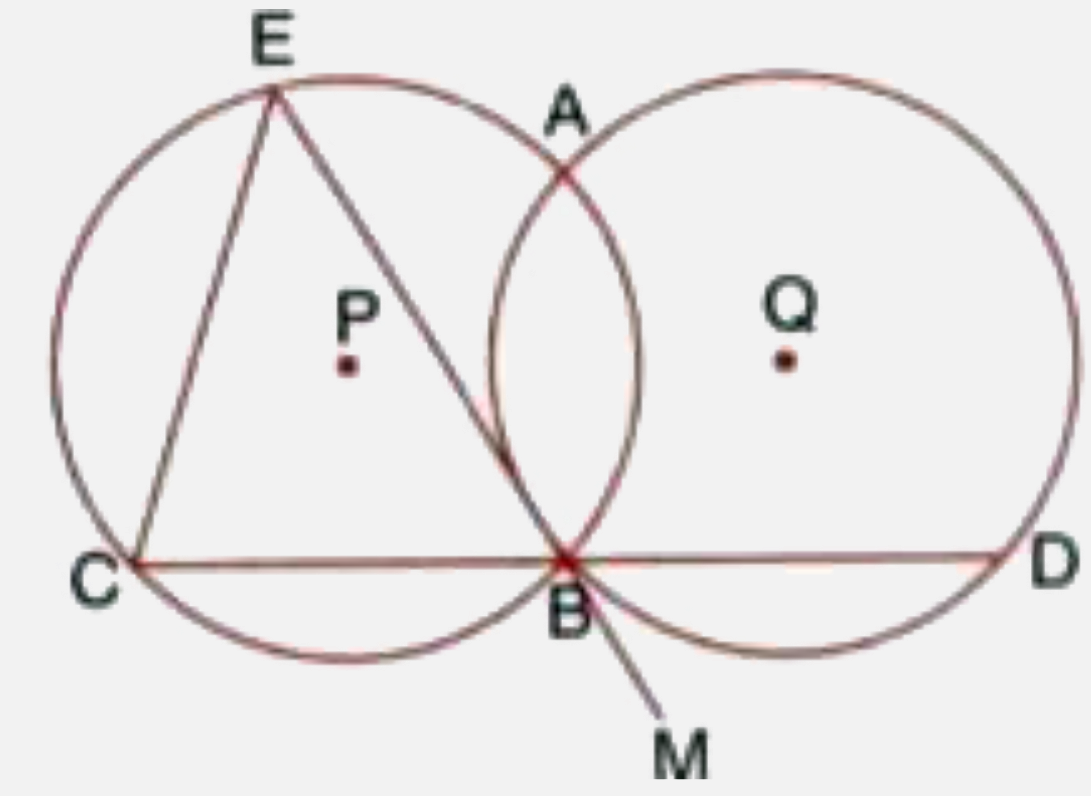
View SolutionAB is the diameter of a circle with centre O. A line PQ touches the given circle at point R and cuts the tangents to the circle through A and B at points P and Q respectively. Prove that ∠POQ=90∘
View Solution
