In Fig.55, if ∠3=610 and ∠7=1180. Is m∣∣n?
To determine whether lines m and n are parallel based on the given angles, we can follow these steps:
1. Identify the Given Angles:
- We have angle 3 = 61° and angle 7 = 118°.
2. Find Angle 4:
- Since angle 3 and angle 4 are on a straight line, we can use the property that the sum of angles on a straight line is 180°.
- Therefore, angle 3 + angle 4 = 180°.
- Substituting the value of angle 3:
61°+angle 4=180°
- Rearranging gives:
angle 4=180°−61°=119°
3. Find Angle 5:
- Angle 7 is given as 118°. Since angle 7 and angle 5 are vertically opposite angles, they are equal.
- Therefore, angle 5 = angle 7 = 118°.
4. Find Angle 6:
- Angle 5 and angle 6 are also on a straight line, so:
- angle 5 + angle 6 = 180°.
- Substituting the value of angle 5:
118°+angle 6=180°
- Rearranging gives:
angle 6=180°−118°=62°
5. Compare Alternate Angles:
- Now we compare angle 3 and angle 6:
- Angle 3 = 61° and angle 6 = 62°.
- Since angle 3 ≠ angle 6, they are not equal.
6. Compare Other Alternate Angles:
- Now we compare angle 4 and angle 5:
- Angle 4 = 119° and angle 5 = 118°.
- Since angle 4 ≠ angle 5, they are also not equal.
7. Conclusion:
- Since neither pair of alternate angles is equal, we conclude that lines m and n are not parallel.
Final Answer:
Lines m and n are not parallel (m || n = No).
- We have angle 3 = 61° and angle 7 = 118°.
- Since angle 3 and angle 4 are on a straight line, we can use the property that the sum of angles on a straight line is 180°.
- Therefore, angle 3 + angle 4 = 180°.
- Substituting the value of angle 3:
61°+angle 4=180°
- Rearranging gives:
angle 4=180°−61°=119°
- Angle 7 is given as 118°. Since angle 7 and angle 5 are vertically opposite angles, they are equal.
- Therefore, angle 5 = angle 7 = 118°.
- Angle 5 and angle 6 are also on a straight line, so:
- angle 5 + angle 6 = 180°.
- Substituting the value of angle 5:
118°+angle 6=180°
- Rearranging gives:
angle 6=180°−118°=62°
- Now we compare angle 3 and angle 6:
- Angle 3 = 61° and angle 6 = 62°.
- Since angle 3 ≠ angle 6, they are not equal.
- Now we compare angle 4 and angle 5:
- Angle 4 = 119° and angle 5 = 118°.
- Since angle 4 ≠ angle 5, they are also not equal.
- Since neither pair of alternate angles is equal, we conclude that lines m and n are not parallel.
Lines m and n are not parallel (m || n = No).
Topper's Solved these Questions
Similar Questions
In Figure, if ∠3=610and ∠7=1180 . Is m∣∣n ?
View SolutionIn Fig. 54, if ∠2=1200 and ∠5=600, show that m∣∣n.
View SolutionIn Figure, transversal l intersects two lines m and n , ∠4=1100 and ∠7=650 . Is m∣∣n?
View SolutionIn ABC, if ∠A=400and ∠B=600. Determine the longest and shortest sides of the triangle.
View SolutionIn the given figure, a transversal n cuts two lines l and m if ∠1=700 and ∠7=800, is l ∣∣ m?
View SolutionIn Fig 66, l∈e lm, ∠1=1200 and ∠2=1000, find out ∠3 and ∠4.
View SolutionIn a ABC, if ∠A=450 and ∠B=700. Determine the shortest and largest sides of the triangle.
View SolutionIn Fig., if l||m||n and ∠1=600, find ∠2.
View SolutionIn Fig.26, AB=AC and ∠ACD=1200. Find ∠A.
View SolutionIn Fig.70. if l||m||n and ∠1=60∘, find ∠2.
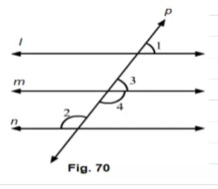
View Solution
