The following pie-chart represents the total number of valid votes obtained by four students who contested for school leadership. The total number of valid votes polled was 720. Answer the following questions by reading the pie-chart.
To solve the problem based on the pie chart representing the valid votes obtained by four students, we will follow these steps:
Step 1: Identify the Central Angles for Each Student
From the pie chart, we need to identify the central angles corresponding to each student. Let's assume the angles are as follows:
- Nashima: 120 degrees
- Suja: 60 degrees
- (Assuming two other students have angles of 100 degrees and 80 degrees)
Step 2: Calculate the Votes for Nashima
To find the number of votes Nashima received, we can use the formula:
Votes=(Central Angle360)×Total Votes
For Nashima:
Votes for Nashima=(120360)×720
Calculating this:
Votes for Nashima=(13)×720=240
Step 3: Calculate the Votes for Suja
Using the same formula for Suja:
Votes for Suja=(60360)×720
Calculating this:
Votes for Suja=(16)×720=120
Step 4: Determine by How Many Votes Nashima Defeated Suja
To find out by how many votes Nashima defeated Suja, we subtract the votes Suja received from the votes Nashima received:
Difference=Votes for Nashima−Votes for Suja
Calculating this:
Difference=240−120=120
Thus, Nashima defeated Suja by 120 votes.
Step 5: Identify the Student with the Minimum Votes
From the angles given, we can see that Suja has the smallest angle (60 degrees). Therefore, Suja received the minimum number of votes, which we calculated as 120 votes.
Final Answers:
1. Nashima defeated Suja by 120 votes.
2. Suja received the minimum number of votes, which is 120.
---
From the pie chart, we need to identify the central angles corresponding to each student. Let's assume the angles are as follows:
- Nashima: 120 degrees
- Suja: 60 degrees
- (Assuming two other students have angles of 100 degrees and 80 degrees)
To find the number of votes Nashima received, we can use the formula:
Votes=(Central Angle360)×Total Votes
For Nashima:
Votes for Nashima=(120360)×720
Calculating this:
Votes for Nashima=(13)×720=240
Using the same formula for Suja:
Votes for Suja=(60360)×720
Calculating this:
Votes for Suja=(16)×720=120
To find out by how many votes Nashima defeated Suja, we subtract the votes Suja received from the votes Nashima received:
Difference=Votes for Nashima−Votes for Suja
Calculating this:
Difference=240−120=120
Thus, Nashima defeated Suja by 120 votes.
From the angles given, we can see that Suja has the smallest angle (60 degrees). Therefore, Suja received the minimum number of votes, which we calculated as 120 votes.
1. Nashima defeated Suja by 120 votes.
2. Suja received the minimum number of votes, which is 120.
Topper's Solved these Questions
Similar Questions
Total number of students of a school in different years is shown in the following table
View SolutionThe following pie-chart represents the amount spent on different sports by a school administration in a calendar year.
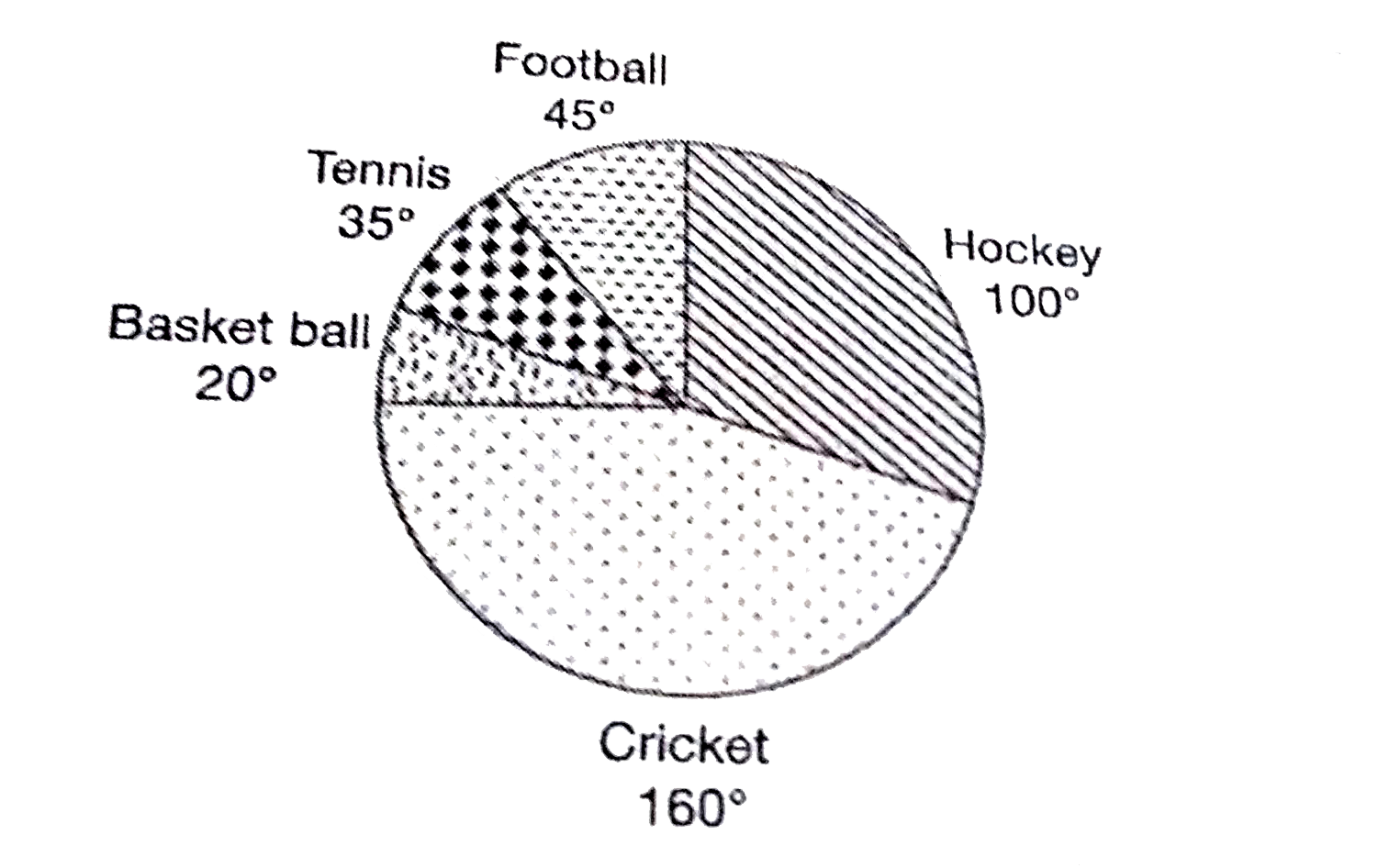
If the money spent on football is Rs. 9000, answer the following questions:
(i) If the amount spent on football was Rs. 9000, then how much more money was spent on hockey than on football ?
(ii) If the amount spent on football Rs. 9000, then what was the total amount spent on all sports ?
View SolutionIn a student election, Rahul got 66 % of the votes polled. If he got 363 votes, find the total number of votes polled.
View SolutionThe following bar graph represents the data for different sizes of shoes worn by the students in a school. Read the graph and answer the following questions.
(i)What are the different numbers of the shoe-worn by the students?
(ii)What is the number of students wearing shoe No. 6?
(iii)Which shoe number is worn by the maximum number of students?
(iv)Which shoe number is worn by the minimum number of students?
View SolutionThe following pie-chart shows the monthly expenditure of a family on food, clothing, rent, miscellaneous expenses and savings. If the family spends Rs. 825 on clothing, answer the following questions: (i) What is the total monthly income of the family? (ii) What percent of the total income does the family save?
View SolutionThe adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.(i) In which subject did the student score 105 marks?(Hint: for 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?)(ii) How many more marks were obtained by the student in Mathematics than in Hindi?(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi (Hint: Just study the central angles).
View SolutionThe following pie-chart gives the marks scored in an examination by a student in various subjects. If the total marks obtained by the student were 540, answer the following questions.
View SolutionThe pie-chart shown in Figure represents the expenditures of a family on different items.If the total annual income of the family is Rs.75,000, Find the expenditure on children education and also find savings by reading the pie-chart.
View SolutionThe following pie-chart shows the number of students admitted in different feculties of a college. If 1000 students are admitted in Science answer the following:
(i) What is the total number of students?
(ii) What is the ratio of students in science and arts?
View SolutionExmine the given graph carefully.
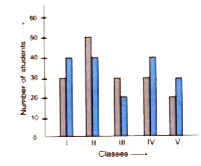
In the graph show above represents the number of girls in a particular class and represents the number of boys in the same class.
Read and answer the following questions.
(i) Which class has the least number of students ?
(ii) Which class has maximum number of students ?
(iii) What is the ratio between the number of girls and the number of boys of class V.
View Solution
