A particle starts from the origin, goes along x-axis to the point (10 m, 0) and then returns along. The same line to the point (-10 m, 0). The distance and displacement of the particle during the trip are
20 m, 0
30 m, 10 m
30 m, - 10 m
20 m, 10 m
The correct Answer is:C
To solve the problem, we need to calculate the distance and displacement of a particle that moves along the x-axis from the origin to the point (10 m, 0) and then returns to the point (-10 m, 0).
1. Identify the Initial and Final Positions:
- The particle starts at the origin, which is the point (0 m, 0).
- It first moves to the point (10 m, 0).
- Then, it returns to the point (-10 m, 0).
2. Calculate the Displacement:
- Displacement is defined as the shortest distance from the initial position to the final position, along with the direction.
- Initial position (O) = (0 m, 0)
- Final position (F) = (-10 m, 0)
- The displacement can be calculated as:
Displacement=Final Position−Initial Position=(−10m)−(0m)=−10m
- The negative sign indicates that the displacement is in the negative x-direction.
3. Calculate the Distance:
- Distance is the total length of the path traveled by the particle.
- The particle travels from (0 m, 0) to (10 m, 0), which is a distance of 10 m.
- Then, it returns from (10 m, 0) to (-10 m, 0). The distance for this part of the journey is:
Distance=10m+10m+10m=30m
- Therefore, the total distance traveled is 30 m.
4. Final Results:
- The displacement of the particle is -10 m.
- The distance traveled by the particle is 30 m.
Conclusion:
- Displacement: -10 m
- Distance: 30 m
- The particle starts at the origin, which is the point (0 m, 0).
- It first moves to the point (10 m, 0).
- Then, it returns to the point (-10 m, 0).
- Displacement is defined as the shortest distance from the initial position to the final position, along with the direction.
- Initial position (O) = (0 m, 0)
- Final position (F) = (-10 m, 0)
- The displacement can be calculated as:
Displacement=Final Position−Initial Position=(−10m)−(0m)=−10m
- The negative sign indicates that the displacement is in the negative x-direction.
- Distance is the total length of the path traveled by the particle.
- The particle travels from (0 m, 0) to (10 m, 0), which is a distance of 10 m.
- Then, it returns from (10 m, 0) to (-10 m, 0). The distance for this part of the journey is:
Distance=10m+10m+10m=30m
- Therefore, the total distance traveled is 30 m.
- The displacement of the particle is -10 m.
- The distance traveled by the particle is 30 m.
- Displacement: -10 m
- Distance: 30 m
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - B)
19 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself
40 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
A particle starts from the origin, goes along the X-axis to the point (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
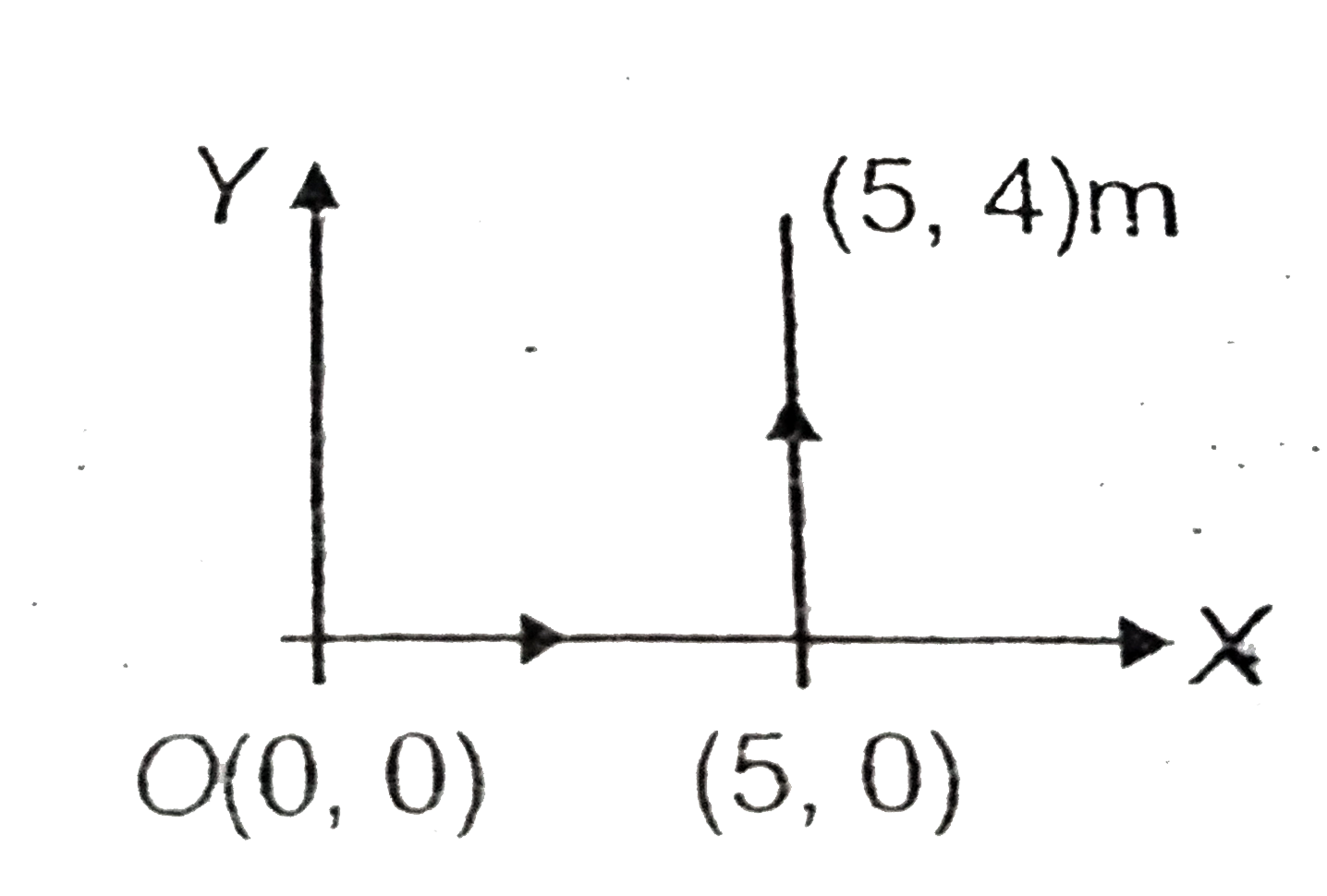
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionA particle starts from origin and moving along x−axis. Whose v−t graph is as shown . Choose the INCORRECT statement :
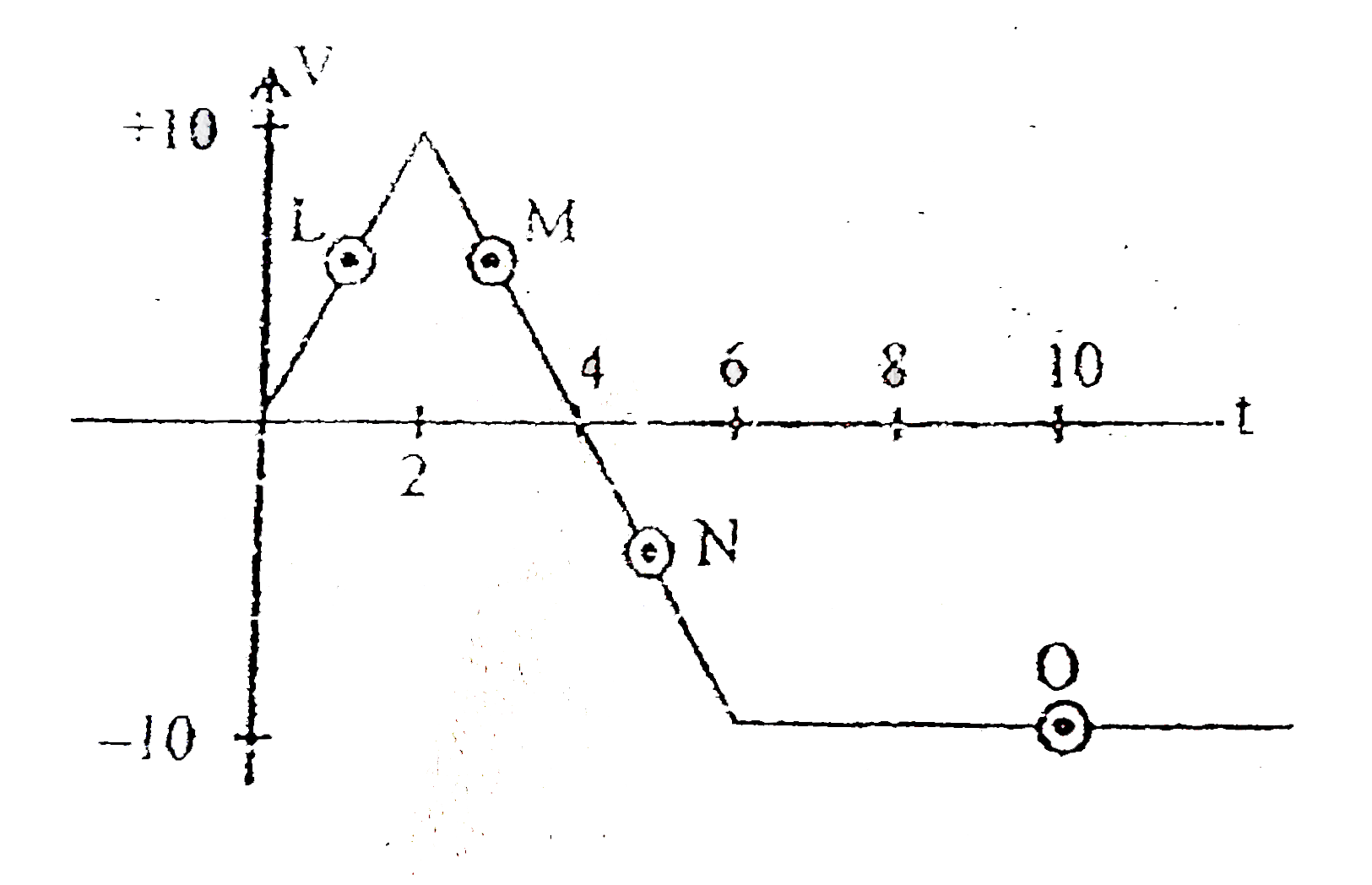 .
.
View SolutionA particle moves on a straight line with velocity 2 m/s covers a distance of 5 m, returns back to initial position along same path with velocity 4 m/s. The distance and displacement covered by particle are respectively.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle is constrained to move on a straight line path. It returns to the starting point after 10 sec . The total distance covered by the particle during this time is 30 m . Which of the following statements about the motion of the particle is false
View SolutionA particle moves from a point (2m,3m,0) to (3m,2m,0) under the action of force of magnitude 5N acting along the line y=x. The work done by the force on the particle during the displacement is
View SolutionTwo particles A and B start from the origin along x-axis. Velocity time graph of both particles are shown in the figure. During the given time interval, the maximum separation between the particles is
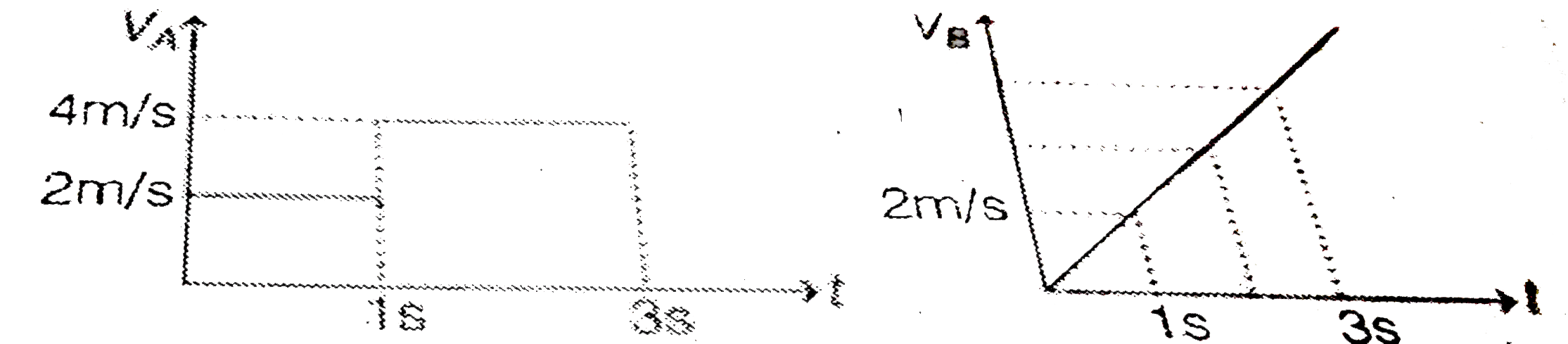
View Solution
