A glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
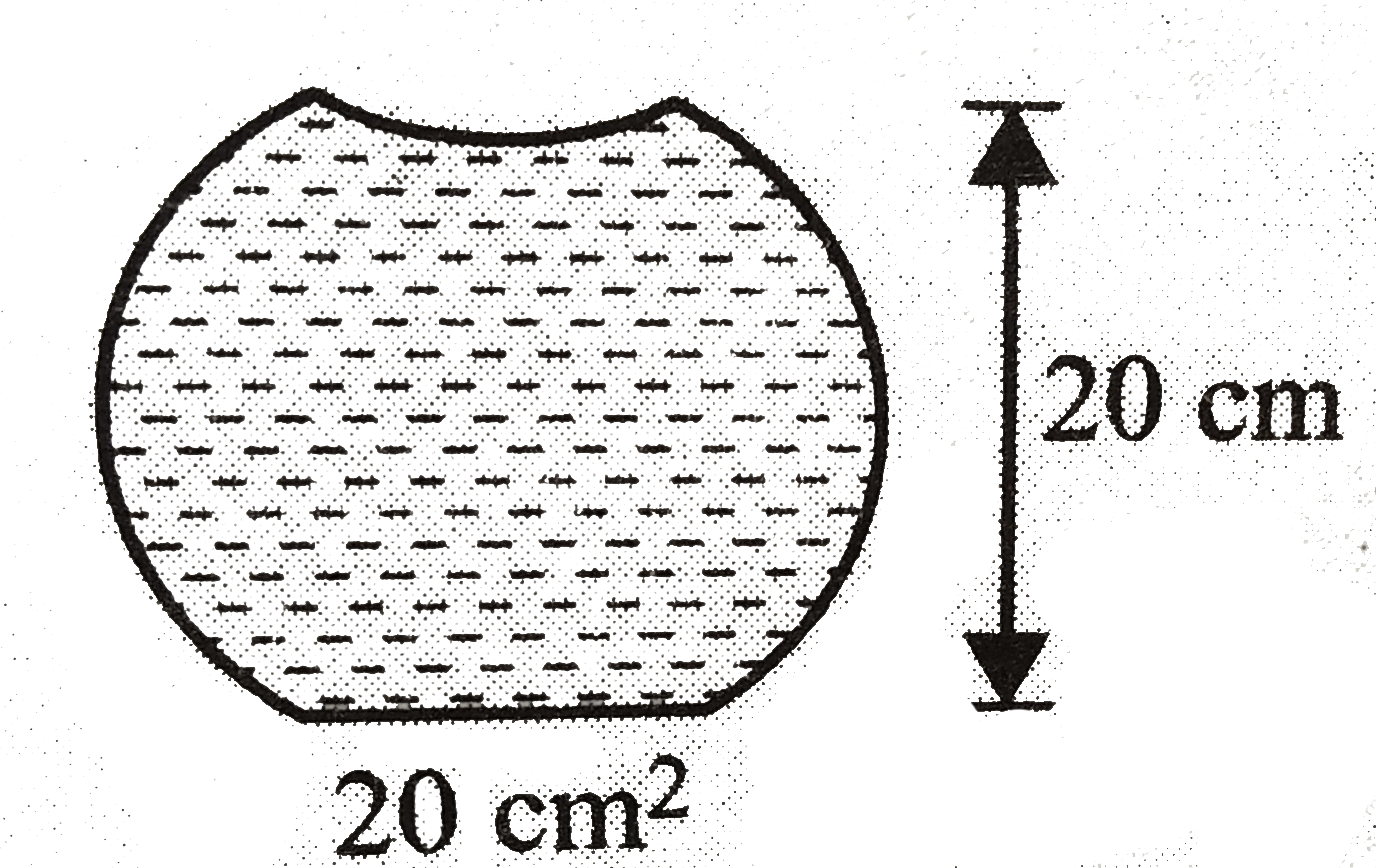
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
The correct Answer is:A, B, D
Pa=1.0×105Nm2,
=Pw=103mgm3
g=10m/s^2<br>v=500m/=500g=0.5kg<br>a.Forceexertedatthe⊥→m=Forcedue→cyl∈drical<br>watercolumn+atm.Force<br>=AxxhxxP_wxxg+P_axxA<br>=A(hrho_wg+P_a)<br>=204N<br>b.Tof∈douttherestant–––––forceexertedbythessoftheglass,omtheeebodydiagramofwater∈stheglass,<br>P_axxA+mg=Axxhxxrho_2xxg+F_s+P_axxA<br>rarr mg=Axxhxxp_wxg+F_s<br>rarr 0.5xx1=20xx10^-4xx20x10^-2xx10^-3xx10+F_s<br>rarr F_s=5-4=1N (upward)
This force 1N is provided by the sides of the glass.
Topper's Solved these Questions
Similar Questions
A glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.
View SolutionA curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
View Solution
Knowledge Check
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]A6B4C2D8
A beaker of circular cross-section of radius 4 cm is filled with mercury up to a height of 10 cm. Find the force exerted by the mercury on the bottom of the beaker. The atmospheric pressure =105Nm−2. Density of mercury =13600kgm−3.Takeg10ms−2
View SolutionAt what depth below the surface of water will pressure be equal to twice the atmospheric pressure ? The atmospheric pressure is 10Ncm−2 , density of water is 103kgm−3 and g=9.8ms−2.
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View SolutionWater is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
View SolutionA gardener waters the plants by a pipe of diameter 1 cm . The water comes out at the rate of 20 cc/s . The reactionary force exerted on the hand of the gardener is
View SolutionThe neck and bottom of a bottle are 3 cm and 15 cm in radius respectively. If the cork is pressed with a force 12 N in the neck of the bottle, then force exerted on the bottom of the bottle is :-
View Solution