Find the force exerted by the water on a 2m2 plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface? Neglect the size of the stone in comparison to the depth of the sea.
The correct Answer is:A
To find the force exerted by the water on a 2 m² plane surface of a large stone placed at the bottom of a sea 500 m deep, we can follow these steps:
Step 1: Understand the Problem
We need to calculate the force exerted by water on a surface at a certain depth. We are given:
- Depth of water (h) = 500 m
- Area of the surface (A) = 2 m²
- Density of water (ρ) = 1000 kg/m³ (standard value)
- Acceleration due to gravity (g) = 10 m/s² (approximate value)
Step 2: Calculate the Pressure at Depth
The pressure (P) at a depth in a fluid is given by the formula:
P=ρgh
Substituting the values:
P=1000kg/m3×10m/s2×500m
Step 3: Perform the Calculation
Calculating the pressure:
P=1000×10×500
P=5000000Pa(Pascals)
Step 4: Calculate the Force
The force (F) exerted by the water on the surface can be calculated using the formula:
F=P×A
Substituting the values:
F=5000000Pa×2m2
Step 5: Perform the Calculation
Calculating the force:
F=5000000×2
F=10000000N
Conclusion
The force exerted by the water on the 2 m² surface of the stone is 107N.
Step 6: Orientation of the Surface
Regarding whether the force depends on the orientation of the surface, we note that pressure at a point in a fluid is the same in all directions. Therefore, the force exerted on the surface does not depend on its orientation, as long as the size of the stone is neglected in comparison to the depth of the sea.
Final Answer
- The force exerted by the water on the surface is 107N.
- The force does not depend on the orientation of the surface.
We need to calculate the force exerted by water on a surface at a certain depth. We are given:
- Depth of water (h) = 500 m
- Area of the surface (A) = 2 m²
- Density of water (ρ) = 1000 kg/m³ (standard value)
- Acceleration due to gravity (g) = 10 m/s² (approximate value)
The pressure (P) at a depth in a fluid is given by the formula:
P=ρgh
Substituting the values:
P=1000kg/m3×10m/s2×500m
Calculating the pressure:
P=1000×10×500
P=5000000Pa(Pascals)
The force (F) exerted by the water on the surface can be calculated using the formula:
F=P×A
Substituting the values:
F=5000000Pa×2m2
Calculating the force:
F=5000000×2
F=10000000N
The force exerted by the water on the 2 m² surface of the stone is 107N.
Regarding whether the force depends on the orientation of the surface, we note that pressure at a point in a fluid is the same in all directions. Therefore, the force exerted on the surface does not depend on its orientation, as long as the size of the stone is neglected in comparison to the depth of the sea.
- The force exerted by the water on the surface is 107N.
- The force does not depend on the orientation of the surface.
Topper's Solved these Questions
Similar Questions
Find the force exerted on a mass of 20 g if the acceleration produced in it is 8m s−2
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionA pond appears to be 2.7 m deep. If the refractive index of water is 43, find the actual depth of the pond.
View SolutionStatement I: Imagine holding two identical bricks under water. Brick A is completely submerged just below the surface of water, while brick B is at a greater depth. The magnitude of force exerted by the person (on the brick) to hold brick B in place is the same as magnitude of force. exerted by the person (on the brick) to hold brick A in place.
Statement II: The magnitude of buoyant force on a brick completely submerged in water is equal to the magnitude of weight of water it displaced and does not depend on the depth of the brick in water.
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
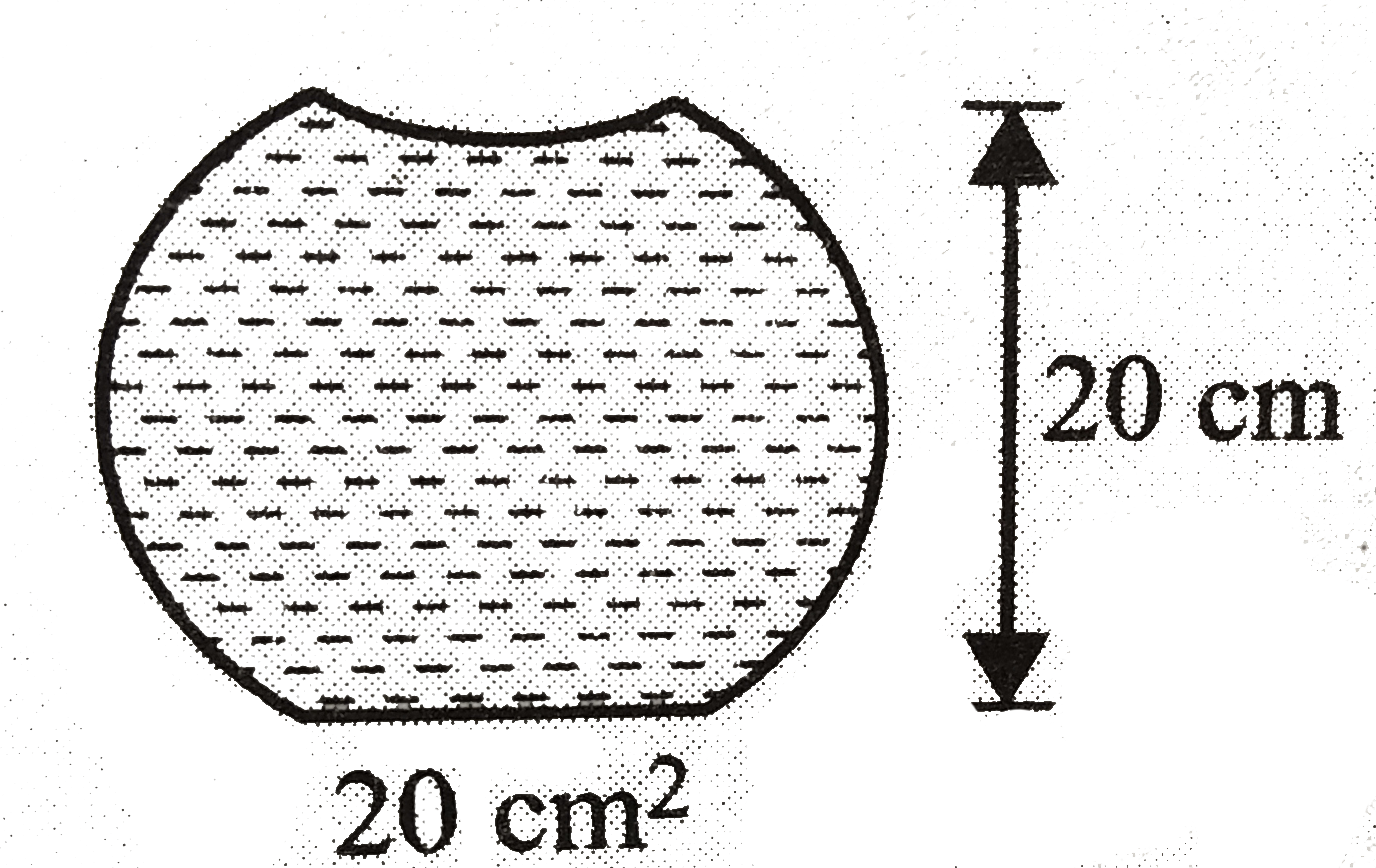
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionA small piece of wood is floating on the surface of a 2.5 m deep lake. Where does the shadow form on the bottom when the sun is just setting? Refractive index of water = 4/3
View SolutionWhen an air bubble of radius 'r' rises from the bottom to the surface of a lake, its radius becomes 5r/4 (the pressure of the atmosphere is equal to the 10m height of water column). If the temperature is constant and the surface tension is neglected, the depth of the lake is
View SolutionIn the arrangement shown in the figure, the pulley has a mass 3m, Neglecting friction on the contact surface, the force exerted by the supporting rope AB on the ceiling is
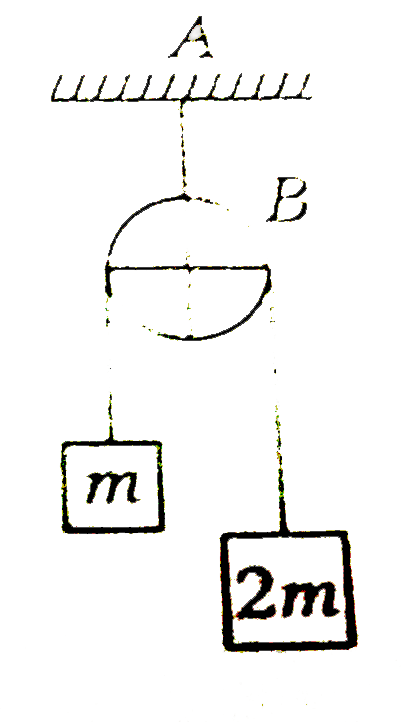
View SolutionA small block B of mass m2 is placed on another block A of mass m1 A constant horizontal force F is applied to the block A. All the surfaces are assumed to be frictionless. Find the acceleration of center of mass of the system
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View Solution