Four modifications are suggested in the lens formula to incude the effect of the thicknes t of the lens. Which one is likely to be correct?
1v−1u=tuf
tv2−1u=1f
1v−t−1v+t=1f
1v−1u+tuv=tf
The correct Answer is:C
To solve the question regarding the modifications in the lens formula to include the effect of the thickness of the lens, we will analyze the four suggested modifications step by step.
Step 1: Understanding the Lens Formula
The basic lens formula is given by:
1f=1v−1u
where:
- f is the focal length of the lens,
- v is the image distance,
- u is the object distance.
This formula assumes that the lens is thin (i.e., its thickness t is negligible).
Step 2: Considering the Thickness of the Lens
When the thickness of the lens is taken into account, we need to modify the lens formula. We will analyze the four suggested modifications to see which one correctly incorporates the thickness t.
Step 3: Analyzing the First Modification
The first modification suggests:
1v−1u=0
This implies that v=u, which does not hold true in general for lenses. Therefore, this modification is incorrect.
Step 4: Analyzing the Second Modification
The second modification suggests:
0v2−1u=1f
This equation is also incorrect as it does not relate to the lens formula and introduces an invalid term. Thus, this modification is also incorrect.
Step 5: Analyzing the Third Modification
The third modification suggests:
1v−0−1v+0=1f
This simplifies to:
1v−1u=1f
This is indeed the original lens formula. However, it does not include the thickness t of the lens, which means this modification is also not valid.
Step 6: Analyzing the Fourth Modification
Assuming the fourth modification suggests a more complex relationship that includes the thickness t in the derivation of the lens formula, we would need to analyze it based on the geometry of the lens and the refraction at the surfaces. However, since we do not have the exact equation, we cannot evaluate it directly.
Conclusion
Based on the analysis of the three modifications provided, the third option is the only one that resembles the original lens formula, but it does not incorporate the thickness of the lens. Therefore, while it is the most correct in terms of structure, it does not fulfill the requirement of including the lens thickness.
Final Answer
The likely correct modification is the third option, but it does not account for the thickness of the lens.
---
The basic lens formula is given by:
1f=1v−1u
where:
- f is the focal length of the lens,
- v is the image distance,
- u is the object distance.
When the thickness of the lens is taken into account, we need to modify the lens formula. We will analyze the four suggested modifications to see which one correctly incorporates the thickness t.
The first modification suggests:
1v−1u=0
This implies that v=u, which does not hold true in general for lenses. Therefore, this modification is incorrect.
The second modification suggests:
0v2−1u=1f
This equation is also incorrect as it does not relate to the lens formula and introduces an invalid term. Thus, this modification is also incorrect.
The third modification suggests:
1v−0−1v+0=1f
This simplifies to:
1v−1u=1f
This is indeed the original lens formula. However, it does not include the thickness t of the lens, which means this modification is also not valid.
Assuming the fourth modification suggests a more complex relationship that includes the thickness t in the derivation of the lens formula, we would need to analyze it based on the geometry of the lens and the refraction at the surfaces. However, since we do not have the exact equation, we cannot evaluate it directly.
Based on the analysis of the three modifications provided, the third option is the only one that resembles the original lens formula, but it does not incorporate the thickness of the lens. Therefore, while it is the most correct in terms of structure, it does not fulfill the requirement of including the lens thickness.
The likely correct modification is the third option, but it does not account for the thickness of the lens.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
78 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
An object is placed at a distance of 30 cm from a concave lens of focal length 30 cm.
(i) Use lens formula to determine the distance of the image from the lens.
(ii) List four characteristics of the image (nature, position, size, erect/inverted) in this case.
(iii) Draw a labelled diagram to justify your answer of part (ii).
View SolutionWhich one is not correct for the effects of deforestation ?
View Solution
Knowledge Check
Which one is the correct formula of aluminium sulphate?
AAlSO4BAl2(SO4)3CAl3(SO4)2DAl(SO4)3
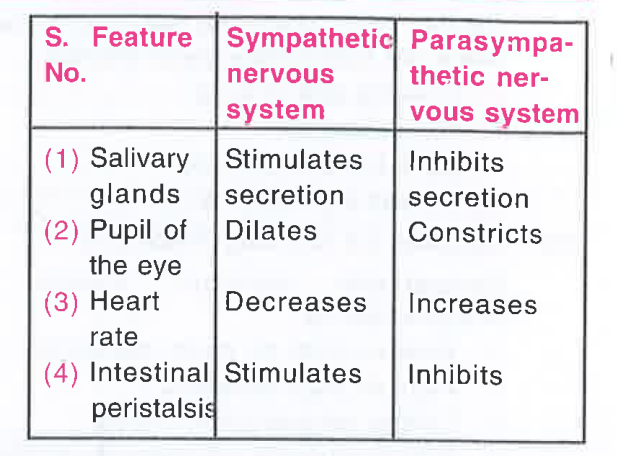
Given below is a table comparing the effects of sympathetic and parasympathetic nervous system for four feature (1-4). Which one feature is correctly described ?
View SolutionWhich type of lens is used to correct astigmatisum ?
View SolutionAn extended object is placed at a distance of 5.0 cm from a convex lens of focal length 8.0 cm. (a) Draw the ray diagram (to the scale) to locate the image and from this, measure the distance of the image from the lens, (b) Find the position of the image from the lens formula and see how close the drawing is to the correct result.
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
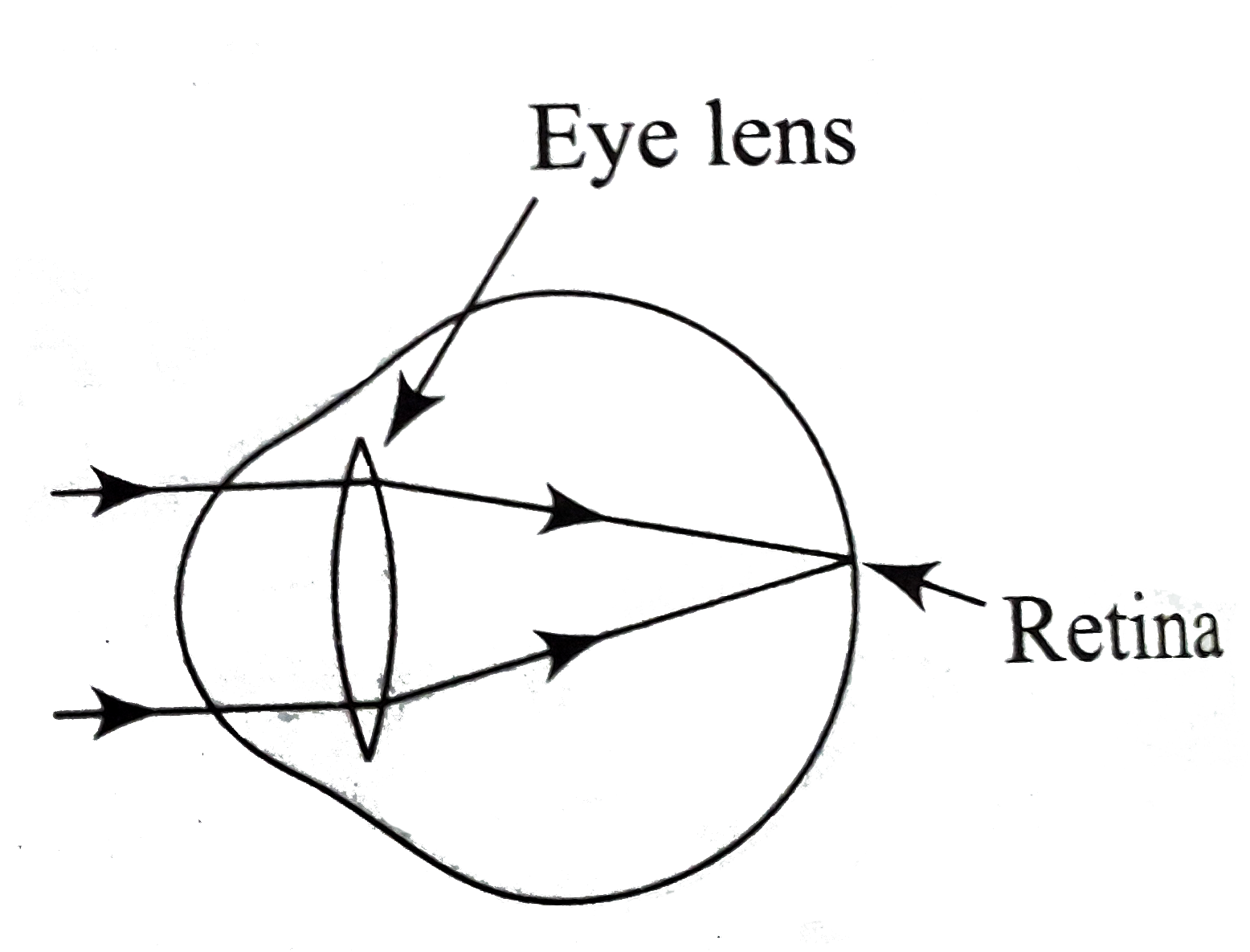
Q. A near sighted man can clearly see ojects only upto a distance of 100cm and not beyond this. The number of the spectacle lenses necessary for the remedy of this defect will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
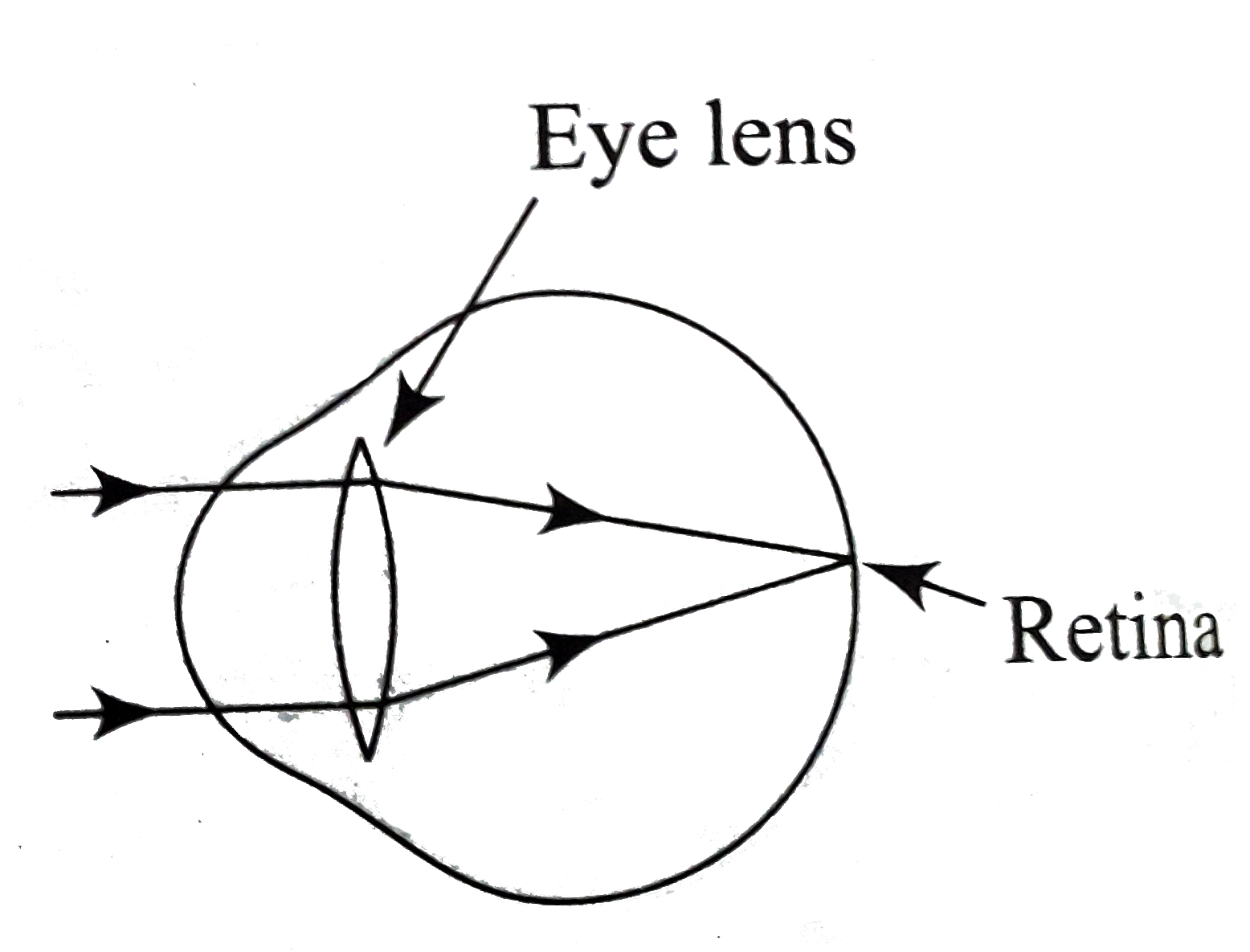
Q. A far sighted man connot see objects clearly unless they are at least 100cm from his eyes. The number of the spectacle lenses that will make his range of clear vision equal to an average grown up person will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
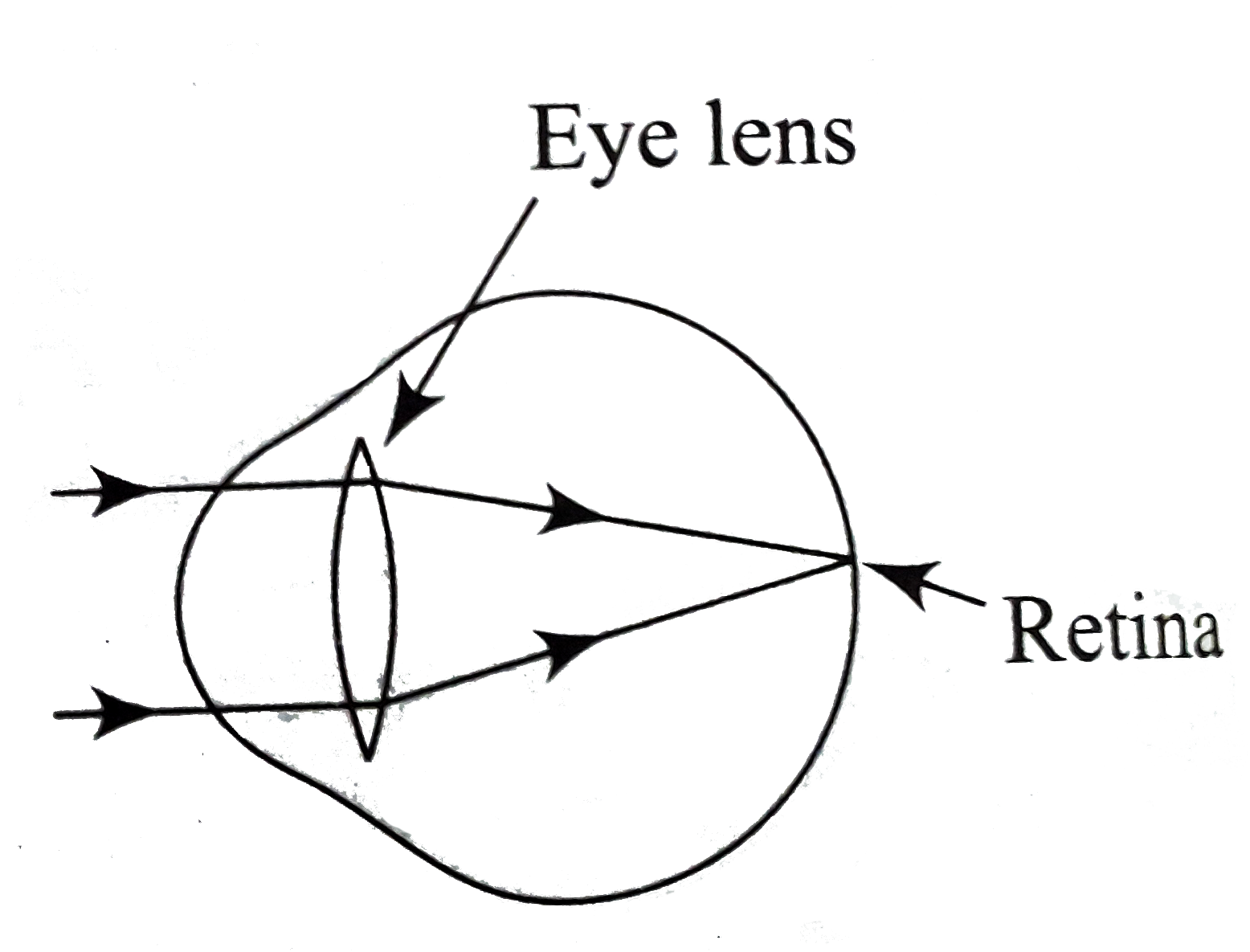
Q. A person can see objects clearly from distance 10cm to ∞. Then, we can say that the person is
View SolutionA body is projected vertically upward from ground. If we neglect the effect of air, then which one of the following is the best representation of variation of speed (v) with time (t)?
View Solution
