A thin lens is made with as material having refractive index μ=1.5. both the sides are convex. It is dipped in water (μ=1.33). It will behave like
a convergent lens
b divergent lens
c rectangular slab
d prism
The correct Answer is:A
To determine how a thin lens behaves when submerged in water, we can analyze the situation step by step.
1. Identify the Refractive Indices:
- The refractive index of the lens material, μL=1.5.
- The refractive index of water, μW=1.33.
2. Determine the Lens Type:
- The lens is a thin lens with both sides convex. In air, a convex lens converges light.
3. Calculate the Focal Length of the Lens in Air:
- The formula for the focal length fL of a lens in air is given by:
1fL=(μL−1)(1R1−1R2)
- For a thin lens with both surfaces convex, we can assume R1=+R and R2=−R:
1fL=(1.5−1)(1R−(−1R))
1fL=0.5(2R)=1R
- Thus, fL=R.
4. Calculate the Focal Length of the Lens in Water:
- When the lens is submerged in water, we need to recalculate the focal length using the refractive index of water:
1fW=(μLμW−1)(1R1−1R2)
- Here, μLμW=1.51.33≈1.13:
1fW=(1.13−1)(1R−(−1R))
1fW=0.13(2R)=0.26R
- Thus, fW=R0.26.
5. Determine the Nature of the Lens:
- Since fW is positive, the lens remains a converging lens even when submerged in water.
6. Conclusion:
- The lens behaves like a converging lens when submerged in water.
Final Answer:
The thin lens behaves like a converging lens when submerged in water.
- The refractive index of the lens material, μL=1.5.
- The refractive index of water, μW=1.33.
- The lens is a thin lens with both sides convex. In air, a convex lens converges light.
- The formula for the focal length fL of a lens in air is given by:
1fL=(μL−1)(1R1−1R2)
- For a thin lens with both surfaces convex, we can assume R1=+R and R2=−R:
1fL=(1.5−1)(1R−(−1R))
1fL=0.5(2R)=1R
- Thus, fL=R.
- When the lens is submerged in water, we need to recalculate the focal length using the refractive index of water:
1fW=(μLμW−1)(1R1−1R2)
- Here, μLμW=1.51.33≈1.13:
1fW=(1.13−1)(1R−(−1R))
1fW=0.13(2R)=0.26R
- Thus, fW=R0.26.
- Since fW is positive, the lens remains a converging lens even when submerged in water.
- The lens behaves like a converging lens when submerged in water.
The thin lens behaves like a converging lens when submerged in water.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
78 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
A thin lens made of glass of refractive index μ=1.5 has a focal length equal to 12 cm in air. It is now immersed in water (μ=43). Its new focal length is
View SolutionA plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View SolutionA double convex lens has two surfaces of equal radii R and refractive index m=1.5, we have
View SolutionA biconcave lens made of a transparent material of refractive index 1.5 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason.
View SolutionA biconcave lens made of a transparent material of refractive index 1.25 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason.
View SolutionA thin bi-convex lens made out of a material of refractive index μ1 is place in a medium of refractive index μ2. A paraxial beam of light, parallel to the principal axis of the lens, is shown in the figure. Based on the ray diagram, we can conclude that

View SolutionA convex lens (refractive index μ = 1.5) has a power P. If it is immersed in a liquid (μ = 4/3), then its power will become/remain
View SolutionA parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
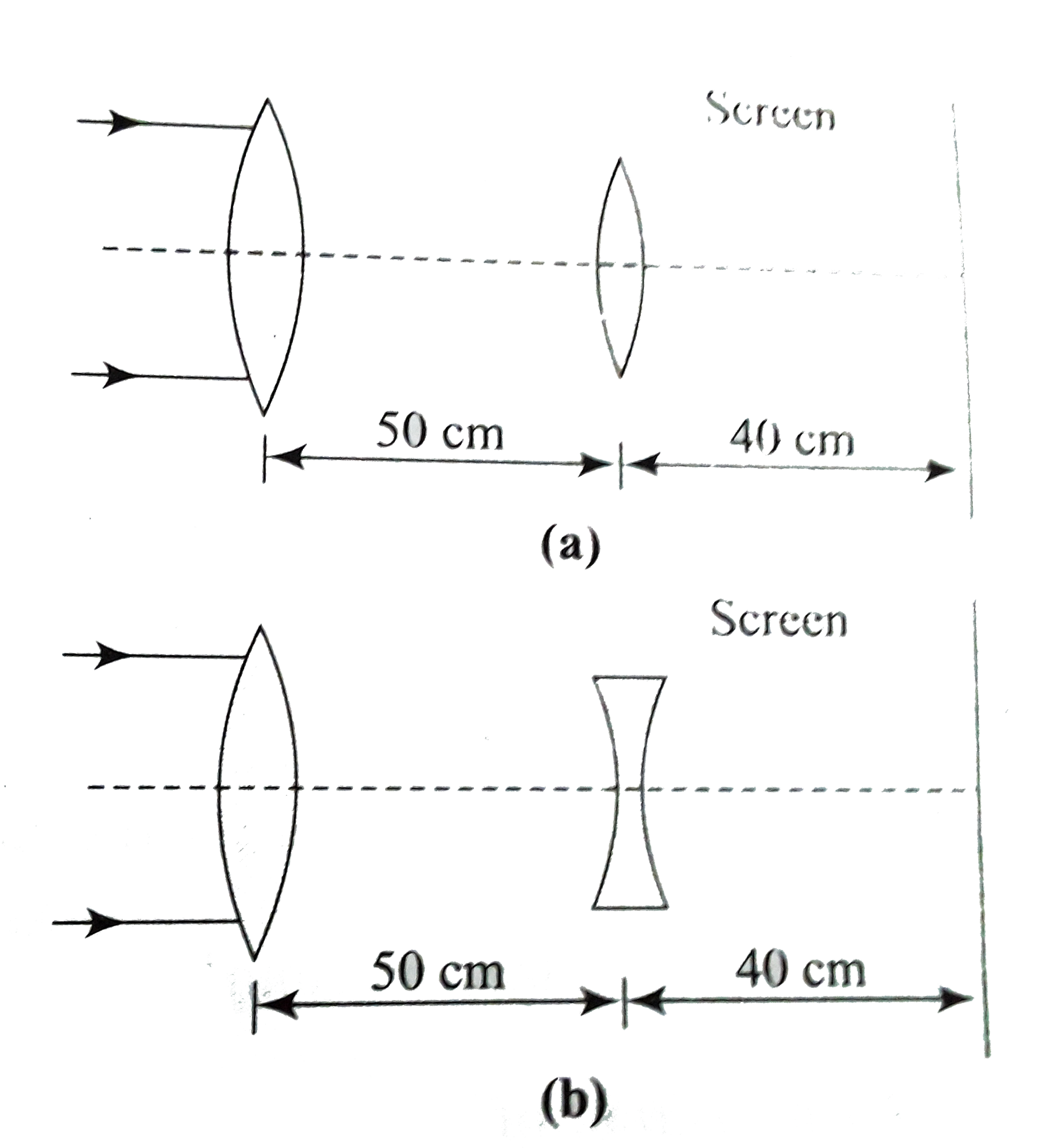
Q. Now, a liquid of refractive index μ is filled to the right of the second lens in case B such that the area illuminated in both the cases is the same. Determing the refractive index of the liquid.
View SolutionA thin lens made of a material of refractive indexμ2 has a medium of refractive index μ1 on one side and a medium of refractive index on the other side. The lens is biconvex and the two radii of curvature have equal magnitude R. A beam of light travelling parallel to the principal axis is incident on the lens. Where will the image be formed if the beam is incident from (a) the medium p, and (b) from the medium μ3?
View SolutionA planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
View Solution
