A wire of length 10cm translates in a direction making an angle of 60∘ with its length. The plane of motion is perpendicular ot a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation of 20 cm s^(-1).
To solve the problem of finding the induced EMF between the ends of a wire translating in a magnetic field, we can follow these steps:
Step 1: Identify the given values
- Length of the wire (L) = 10 cm = 0.1 m
- Speed of translation (v) = 20 cm/s = 0.2 m/s
- Magnetic field strength (B) = 1.0 T
- Angle (θ) = 60°
Step 2: Write the formula for induced EMF
The induced EMF (ε) in a wire moving in a magnetic field can be calculated using the formula:
ϵ=B⋅L⋅v⋅sin(θ)
Step 3: Substitute the known values into the formula
Substituting the values we have:
- B = 1.0 T
- L = 0.1 m
- v = 0.2 m/s
- θ = 60°
We also need to calculate sin(60°):
sin(60°)=√32
Now substituting everything into the formula:
ϵ=1.0⋅0.1⋅0.2⋅√32
Step 4: Calculate the induced EMF
Calculating step-by-step:
ϵ=1.0⋅0.1⋅0.2⋅√32
=0.1⋅0.2⋅√32
=0.02⋅√32
=0.02√32
=0.01√3
Step 5: Final result
Thus, the induced EMF is:
ϵ=√3×10−2 volts
- Length of the wire (L) = 10 cm = 0.1 m
- Speed of translation (v) = 20 cm/s = 0.2 m/s
- Magnetic field strength (B) = 1.0 T
- Angle (θ) = 60°
The induced EMF (ε) in a wire moving in a magnetic field can be calculated using the formula:
ϵ=B⋅L⋅v⋅sin(θ)
Substituting the values we have:
- B = 1.0 T
- L = 0.1 m
- v = 0.2 m/s
- θ = 60°
sin(60°)=√32
ϵ=1.0⋅0.1⋅0.2⋅√32
Calculating step-by-step:
ϵ=1.0⋅0.1⋅0.2⋅√32
=0.1⋅0.2⋅√32
=0.02⋅√32
=0.02√32
=0.01√3
Thus, the induced EMF is:
ϵ=√3×10−2 volts
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A metallic metre stick translates in a direction making an angle of 60∘ with its length.The plane of motion is perpendicular to a uniform magnetic field of 0.1T that exists in the space.Find the emf induced between the ends of the rod if the speed of translation is 0.2m/s.
View SolutionA conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
View SolutionA metallic wire PQ of length 1cm moves with a velocity of 2m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2T.Find the emf induced between the ends of the wire.Which end will be positively charged.
 View Solution
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
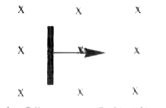 View Solution
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
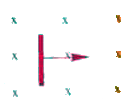 View Solution
View SolutionA metallic metre sitck moves with a velocity of 2 ms ^(-1) in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf indcued between the ends of the stick.
View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View SolutionA wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
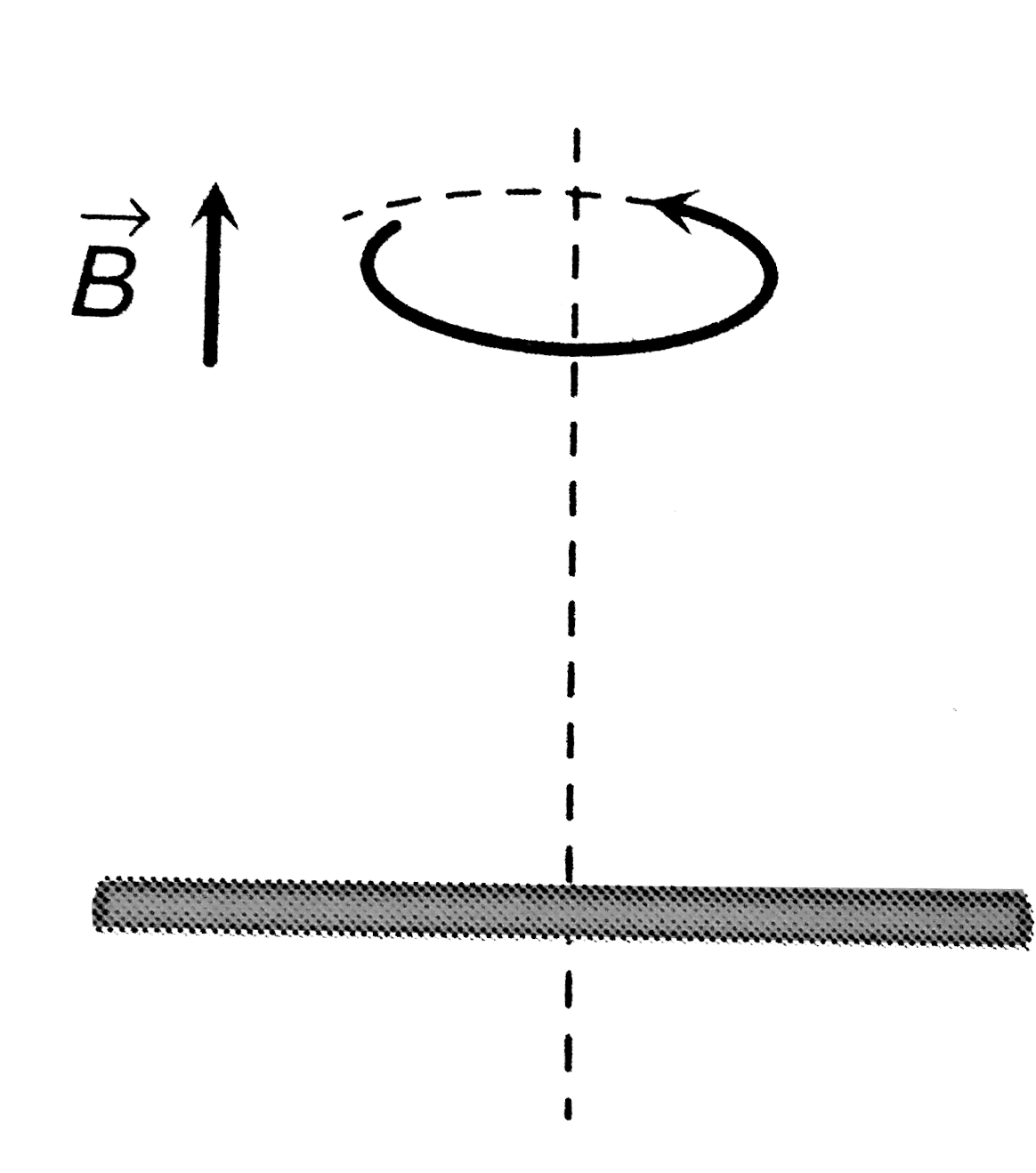 View Solution
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
 View Solution
View Solution

