an inductor of inductance 2.00 H is joined in series with a resistor of resistance 200Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) th current in the circuit, (b) the power delivered by the batter, (c ) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
Here L=2H,R=200W,
E=2V,t=10ms
(a)i=i0(1−e−t/(τ))
=2200(1−e−10×10−8×2002)
=0.01(1−e−1)
0.01×0.632=6.3mA
(b) Power delivered by the battery
P=Vi
P=Ei0(1−e−t/(τ))
P=2×2200(1−e10×10−3×2002)
P=0.02(1−e−1)
=0.01264=12mW.
(c)Powerdissipated∈theresis→r=i2R
=[i_(0)(1-e^(-t//(tau)))]^(2) R<br>=(6.3xx6.3xx200xx10^(-5))<br>=79.38xx10^(-4)<br>=7.938xx10^(-3)=8mW.<br>(d)Rateatwhiche≠rgyiss→red∈themag≠ticfield=(12)(Li2)
=(L2)(i0)2(1−e−t/(τ))2
=2xx10^(-2)(0.225)<br>=0.455xx10^(-2)<br>=4.6×10−3
=4.6mW.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A capacitor of capacitance 12(μ)Fis connected to a battery of emf 6.00V and internal resistance 1.00(Ω)through resistanceless leads. 12.0(mu)s after the connections are made, what will be (a) the current in the circuit, (b)the power delivered by the battery ,(c)the power dissipated in heat and (d)the rate at which the energy stored in the capacitor is increasing.
View SolutionA capacitor of capacitance 12(μ)Fis connected to a battery of emf 6.00V and internal resistance 1.00(Ω)through resistanceless leads. 12.0(mu)s after the connections are made, what will be (a) the current in the circuit, (b)the power delivered by the battery ,(c)the power dissipated in heat and (d)the rate at which the energy stored in the capacitor is increasing.
View Solution
Knowledge Check
- Question 1 - Select One
A current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is
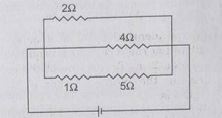 A4WB2WC1WD5W
A4WB2WC1WD5W - Question 2 - Select One
A current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is
 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 watt
A capacitor of capacitance 10μF is connected to a resistance 2Ω and a battery of emf 5V of negligible interanl resistance. After 20μs of comleting the circuit find.
a. power delivered by the battery
b. power dissipated as heat
c. rate of energy stored in the capacitorView SolutionA capacitor of capacitance 10μF is connected to a resistance 2Ω and a battery of emf 5V of negligible interanl resistance. After 20μs of comleting the circuit find.
a. power delivered by the battery
b. power dissipated as heat
c. rate of energy stored in the capacitorView SolutionA 50 mH inductor is in series with a 10 ohm resistor and a battery with an emf of 25 V. At t = 0 the switch is closed. Find
the power dissipated in the resistorView SolutionA3 H inductor is placed in series with 10Ω resistor and an emf of 10V is applied to the combination. Find
(i) the current at 0.3s,
(ii) the rate of increase of current at 0.3s,
(iii) the rate at which energy is dissipated as heat at t=0.3s.
(iv) the rate at which energy is stored in the magnetic field at 0.3s.
(v) the rate at which energy is delivered by the battery, and
(vi) the energy stored when the current has attained steady value.View Solution5 A 50 mH inductor is in series with a 10 2 resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find
Q(d) the power dissipated in the resistorView SolutionAn inductor of inductance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
View Solution

