A rod of mass 'M' and length '2L' is suspended at its middle by a wire. It exhibits torsional oscillations, if two masses each of 'm' are attached at distance'L/2' from its centre on both sides, it reduces the oscillation frequency by 20%. The value of ratio m/M is close to :
0.77
0.57
0.37
0.17
To solve the problem, we need to analyze the effect of adding two masses to the rod on its oscillation frequency. We will use the relationship between the moment of inertia and the frequency of torsional oscillations.
1. Understanding the Problem:
- A rod of mass M and length 2L is suspended at its middle.
- Two masses m are attached at a distance L2 from the center on both sides.
- The addition of these masses reduces the oscillation frequency by 20%.
2. Frequency and Moment of Inertia:
- The frequency ω of torsional oscillations is related to the moment of inertia I by the formula:
ω∝√KI
where K is the torsional constant (which remains constant in this case).
3. Setting Up the Frequencies:
- Let ω1 be the initial frequency (without masses) and ω2 be the frequency after adding the masses.
- Since the frequency is reduced by 20%, we have:
ω2=0.8ω1
4. Relating the Moments of Inertia:
- The square of the frequencies gives us:
(ω2ω1)2=I1I2
- Substituting ω2=0.8ω1:
(0.8)2=I1I2⟹0.64=I1I2
5. Calculating the Moments of Inertia:
- The moment of inertia of the rod I1 (without masses) is:
I1=M(2L)212=M⋅4L212=ML23
- The moment of inertia of the two masses m attached at a distance L2 from the center is:
Im=2⋅m(L2)2=2⋅m⋅L24=mL22
- Therefore, the total moment of inertia I2 (with masses) is:
I2=I1+Im=ML23+mL22
6. Setting Up the Equation:
- We can now set up the equation using the relationship we derived:
0.64=I1I2=ML23ML23+mL22
- Cancel L2 from numerator and denominator:
0.64=M3M3+m2
7. Cross-Multiplying:
- Cross-multiplying gives:
0.64(M3+m2)=M3
- Expanding this:
0.64⋅M3+0.32m=M3
8. Rearranging the Equation:
- Rearranging gives:
0.32m=M3−0.64⋅M3=M3⋅(1−0.64)=M3⋅0.36
- Therefore:
m=0.36M0.32=9M8
9. Finding the Ratio:
- The ratio mM is:
mM=98M⋅M=98
Final Answer:
The value of the ratio mM is close to 0.375.
- A rod of mass M and length 2L is suspended at its middle.
- Two masses m are attached at a distance L2 from the center on both sides.
- The addition of these masses reduces the oscillation frequency by 20%.
- The frequency ω of torsional oscillations is related to the moment of inertia I by the formula:
ω∝√KI
where K is the torsional constant (which remains constant in this case).
- Let ω1 be the initial frequency (without masses) and ω2 be the frequency after adding the masses.
- Since the frequency is reduced by 20%, we have:
ω2=0.8ω1
- The square of the frequencies gives us:
(ω2ω1)2=I1I2
- Substituting ω2=0.8ω1:
(0.8)2=I1I2⟹0.64=I1I2
- The moment of inertia of the rod I1 (without masses) is:
I1=M(2L)212=M⋅4L212=ML23
- The moment of inertia of the two masses m attached at a distance L2 from the center is:
Im=2⋅m(L2)2=2⋅m⋅L24=mL22
- Therefore, the total moment of inertia I2 (with masses) is:
I2=I1+Im=ML23+mL22
- We can now set up the equation using the relationship we derived:
0.64=I1I2=ML23ML23+mL22
- Cancel L2 from numerator and denominator:
0.64=M3M3+m2
- Cross-multiplying gives:
0.64(M3+m2)=M3
- Expanding this:
0.64⋅M3+0.32m=M3
- Rearranging gives:
0.32m=M3−0.64⋅M3=M3⋅(1−0.64)=M3⋅0.36
- Therefore:
m=0.36M0.32=9M8
- The ratio mM is:
mM=98M⋅M=98
The value of the ratio mM is close to 0.375.
Similar Questions
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its Centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View SolutionA rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
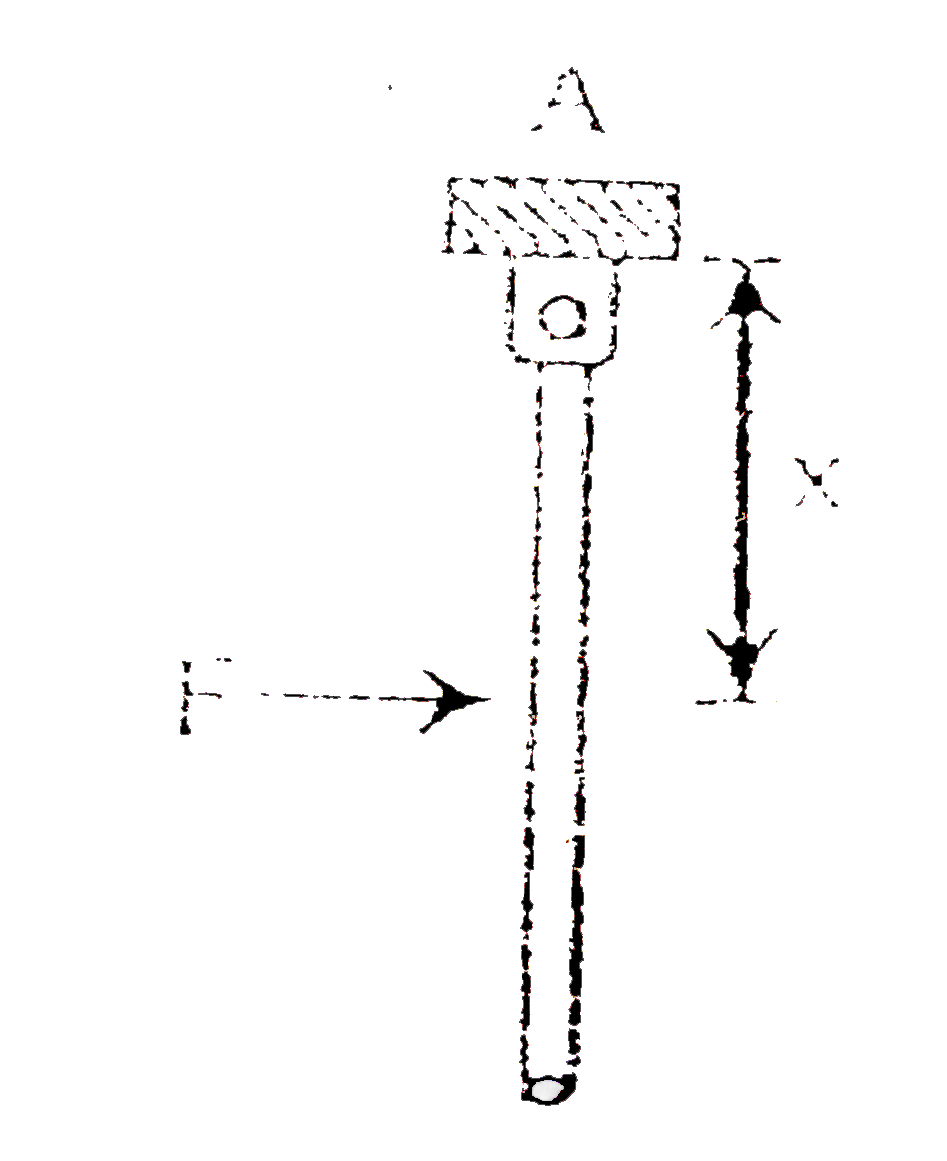
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
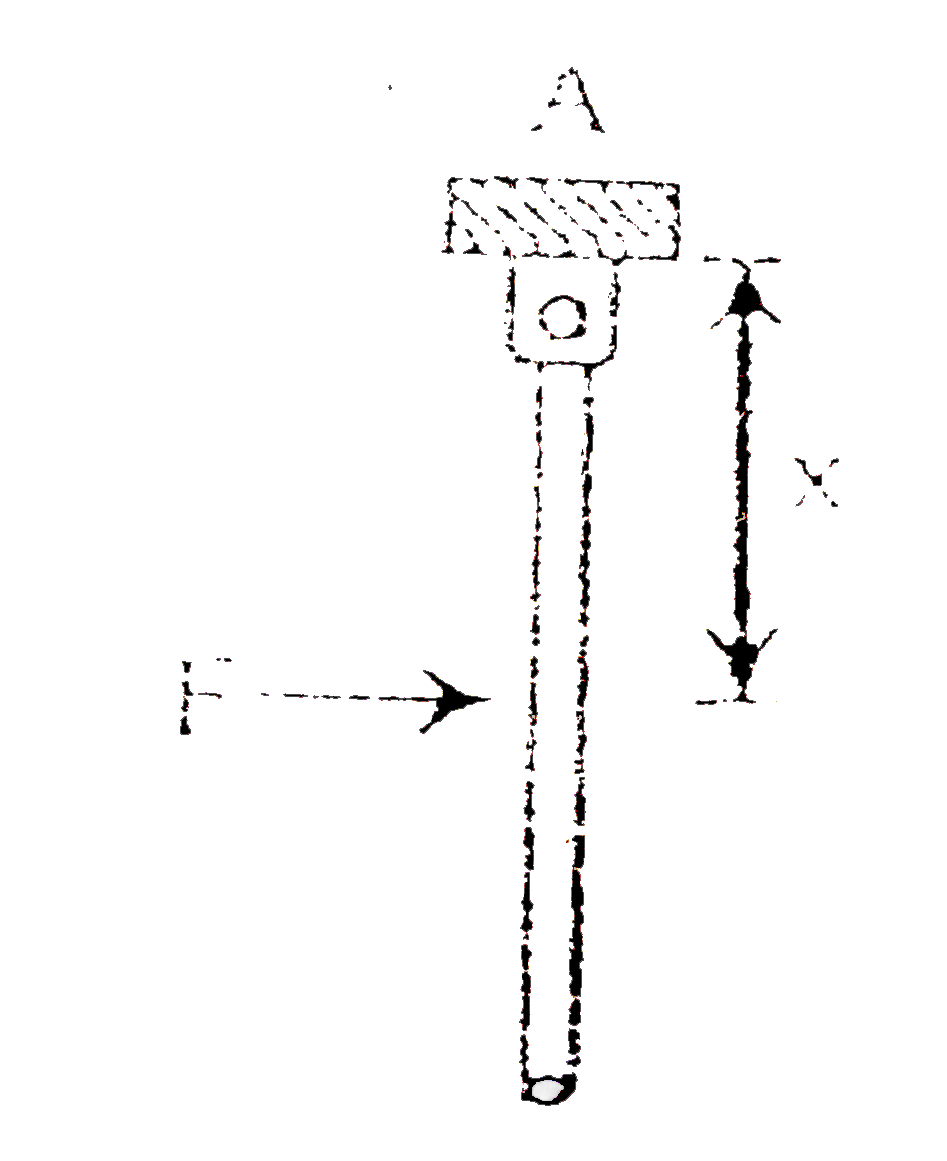
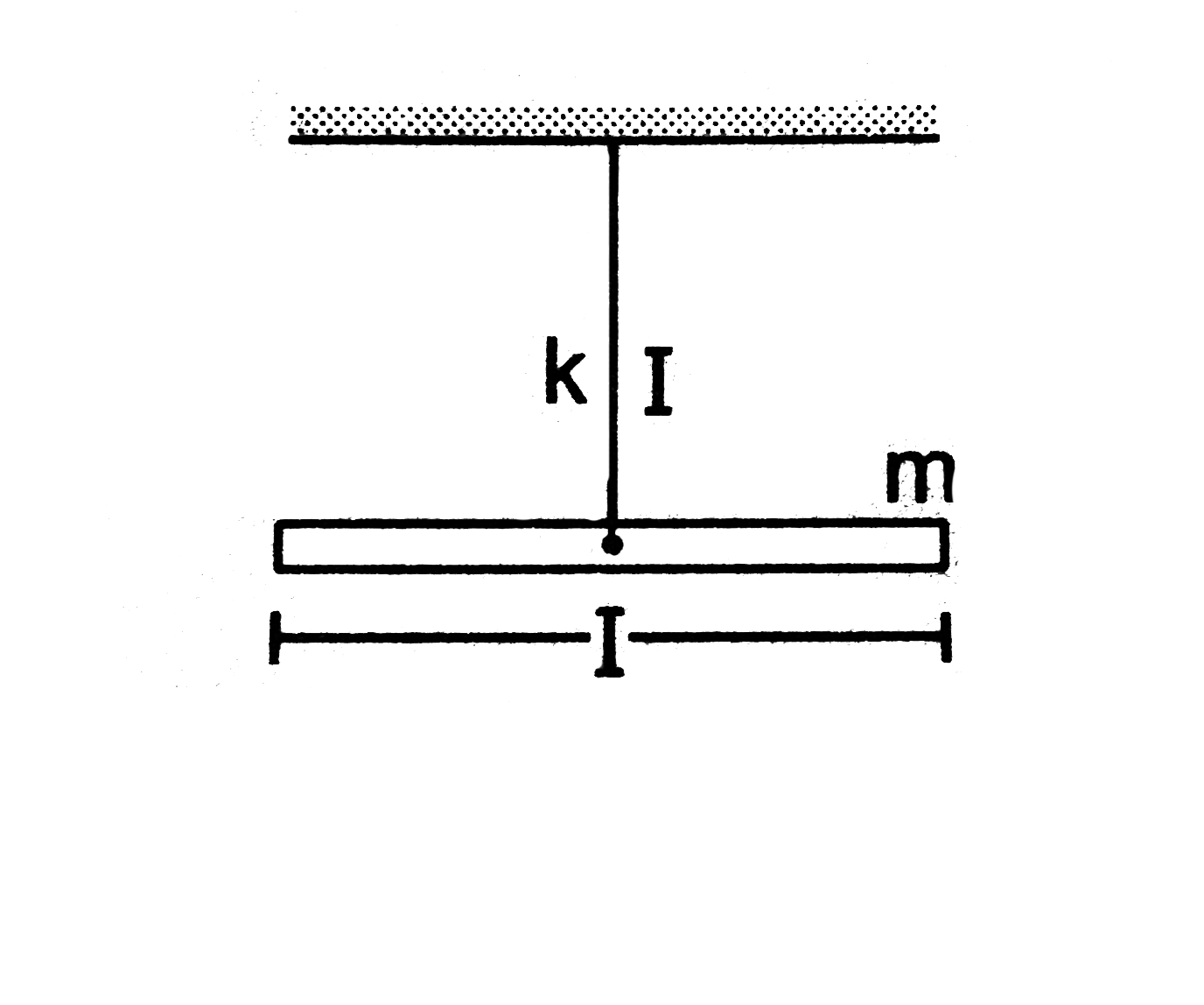
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA thin rod of mass m and length l is suspended from one of its ends. It is set into oscillation about a horizontal axis. Its angular speed is ω while passing through its mean position. How high will its centre of mass rise from its lowest position ?
View SolutionThe frequency of oscillation of amass m suspended by a spring is v1. If length of spring is cut to one third then the same mass oscillations with frequency v2. Then
View Solution
