A mass m attached to spring of natural length l0 and spring constant k. One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k>>mω2 ) :
mω22k
2mω2k
mω2k
√23(mω2k)
The correct Answer is:3
To solve the problem, we need to find the extension per unit length in the spring when a mass m is attached to it and the spring is subjected to a centrifugal force due to the rotation of a disc at a constant angular speed ω.
1. Identify the Forces Acting on the Mass:
- The mass m experiences a centrifugal force due to the rotation of the disc, which can be expressed as:
Fcentrifugal=mω2r
- Here, r is the total length from the center of the disc to the mass, which is given by:
r=l0+x
- Where l0 is the natural length of the spring and x is the extension of the spring.
2. Write the Equation for the Spring Force:
- The spring exerts a restoring force given by Hooke's Law:
Fspring=kx
- Where k is the spring constant.
3. Set Up the Equation of Motion:
- At equilibrium, the centrifugal force is balanced by the spring force:
kx=mω2(l0+x)
4. Rearranging the Equation:
- Expanding the right side gives:
kx=mω2l0+mω2x
- Rearranging this equation leads to:
kx−mω2x=mω2l0
- Factoring out x from the left side:
x(k−mω2)=mω2l0
5. Solve for x:
- We can solve for x:
x=mω2l0k−mω2
6. Find the Extension per Unit Length:
- We need to find the extension per unit length, which is xl0:
xl0=mω2k−mω2
7. Apply the Given Condition k≫mω2:
- Since k is much greater than mω2, we can approximate:
k−mω2≈k
- Therefore, the expression simplifies to:
xl0≈mω2k
Final Result:
The extension per unit length in the spring is given by:
xl0=mω2k
- The mass m experiences a centrifugal force due to the rotation of the disc, which can be expressed as:
Fcentrifugal=mω2r
- Here, r is the total length from the center of the disc to the mass, which is given by:
r=l0+x
- Where l0 is the natural length of the spring and x is the extension of the spring.
- The spring exerts a restoring force given by Hooke's Law:
Fspring=kx
- Where k is the spring constant.
- At equilibrium, the centrifugal force is balanced by the spring force:
kx=mω2(l0+x)
- Expanding the right side gives:
kx=mω2l0+mω2x
- Rearranging this equation leads to:
kx−mω2x=mω2l0
- Factoring out x from the left side:
x(k−mω2)=mω2l0
- We can solve for x:
x=mω2l0k−mω2
- We need to find the extension per unit length, which is xl0:
xl0=mω2k−mω2
- Since k is much greater than mω2, we can approximate:
k−mω2≈k
- Therefore, the expression simplifies to:
xl0≈mω2k
The extension per unit length in the spring is given by:
xl0=mω2k
Topper's Solved these Questions
Similar Questions
A block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
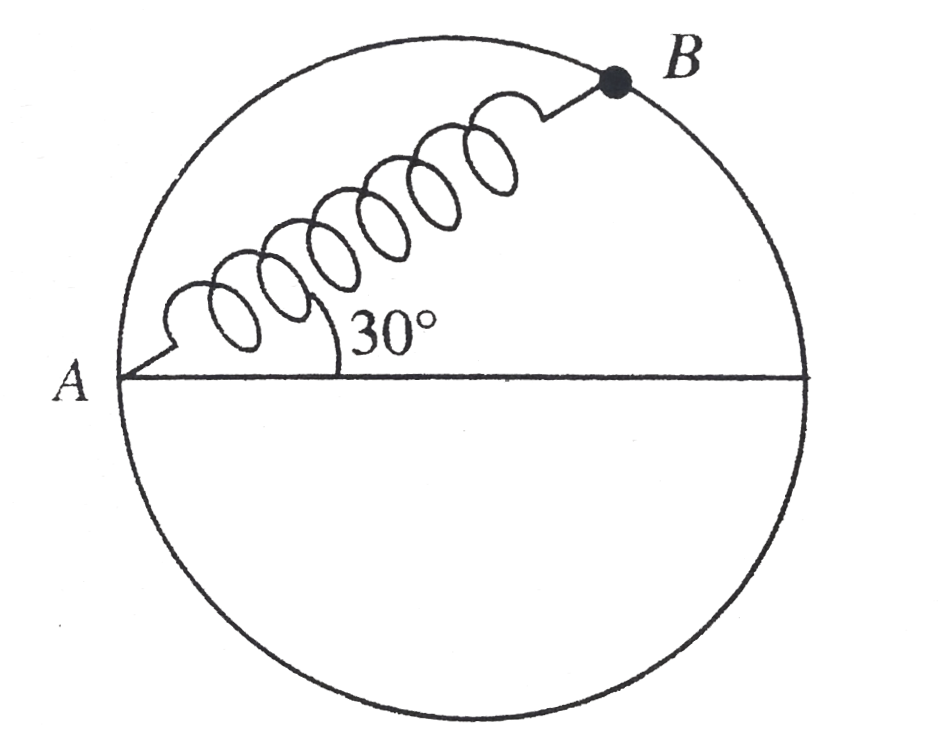
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
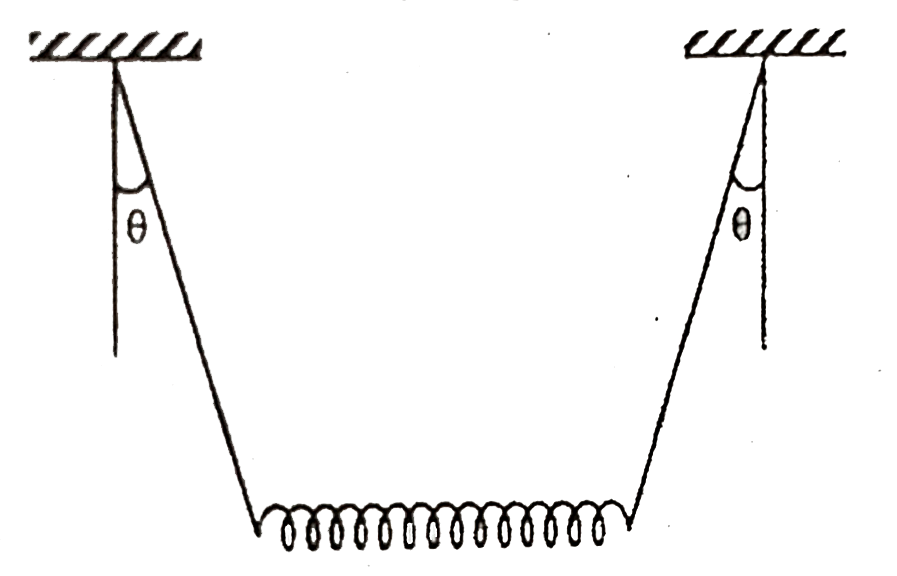
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
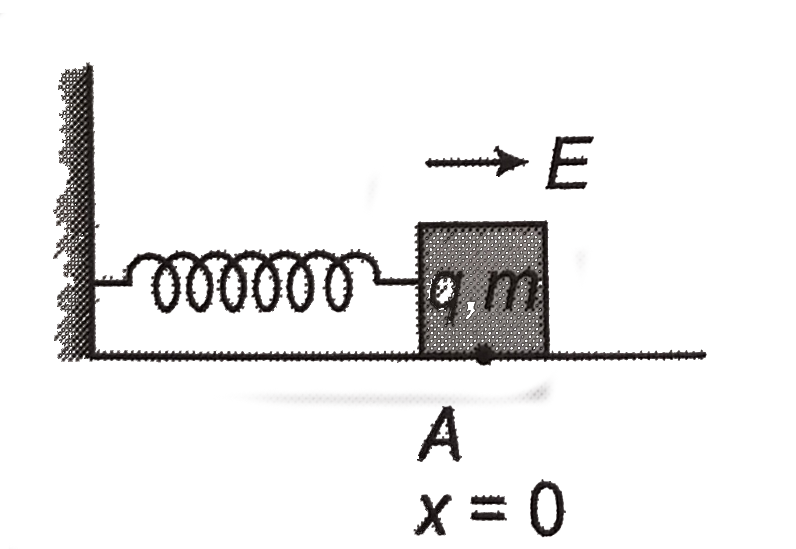
View SolutionA block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
View SolutionA massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
View Solution
