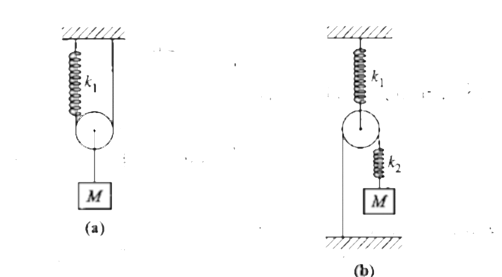
Find the stretch in the springs shown in figure. The respective data are given in the figure. The friction and masses in pulleys are negligible. Find the extension in spring?

a) As mass M is in equilibrium, the tension in the string with which it is hanging will be Mg. As pulley is massless the tension in the upper string must be half of the lower string, Mg/2. The stretch in the spring must be such that the restoring force in the string is equal to the tension in it. Thus we have
k1x=Mg2orx1=Mg2k1
(b) Here again mass M is in equilibrium, thus the tension in the string connected to it must be equal to Mg and hence the restoring force in the lower spring will also be Mg. If x1 be the extension in this spring, we have
k1x1=Mgorx1=Mgk1
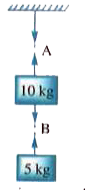
As pulley is light, the tension in upper string must be twice that of the lower srting, 2Mg which is equal to restoring force in the upper spring. If x1 is the extension in the upper spring, we have
k2x2=Mgorx2=2Mgk2
Wherever a body is in equilibrium, due to inertia it is maintained in a state of rest. If any of the supporting force a body is removed, body start from rest with some acceleration in the direction opposite to the force applied by the support, as all other forces acting on body will have a resultant in that direction.
We discuss the situation with an example shown in figure. Two masses 5 kg and 10 kg are hanging in equilibrium with the strings A and B. If tensions in the strings A and B are T1andT2 respectively, then we have
T1=5g=50N,T2=15g=150N
If at some instant we break string B. tension T1 becomes zero instantane-ously and block will start falling from rest under gravity and 10 kg block, as it is still in equilibrium, T2 will instantly change to 10 N to balance its weight.
If instead of string B, we break the string A, tension T2 becomes zero and both the blocks will start falling with acceleration g.
Now T1 is just an internal force for the system of two blocks and as there is no interaction between the two blocks and both are falling under gravity T1 will also instantly become zero.
Now to understand the concept in a better way we slightly modify the situation of previous example. Instead of strings, we use springs as shown in figure. Initially the blocks are in equilibrium . If spring B breaks, its tension will instantly become zero as we are using ideal springs (massless/ inertialess),but due to inertia initially 10kg mass will not move from its initial position, so tension in upper spring will not change instantly hence it will accelerate in upward direction with acceleration given as
a=150−10010=5m/s2
If spring A breaks tension in spring A will instantly become zero, but as due to inertia 5 kg and 10 kg blocks will start moving from rest. As initally just after breaking of spring A the two masses are at rest, tension in spring B will not change at this instant which is T = 5g =50 N,
Thus at this instant (just after spring A is cut)
acceleration of 10 kg mass is a1=10g+kx10=100+5010=15m/s2
and that of 5 kg mass is a2=5g−kx5=50−505=0m/sec2

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - LONG ANSWER TYPE QUESTIONS
2 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - SHORT ANSWER TYPE QUESTION
2 Videos
- KINETIC THEORY OF GASESBOOK - AAKASH SERIESCHAPTER - KINETIC THEORY OF GASESEXERCISE - Practice Exercise
15 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-3
43 Videos
Similar Questions
Find the stretch in the springs shown in figure-2.112. The respective data are given in the figure. The friction and masses in pulleys are negligible.
View SolutionFind the reading of th spring balance shown in figure. The elevator is going up with an accelertion of g/10, the pulley and the strng are light and the pulley is smooth.
View Solution
Knowledge Check
Find maximum compression is the spring from the given figure.
 A√25mB16√25mC3√25mD6√25m
A√25mB16√25mC3√25mD6√25m
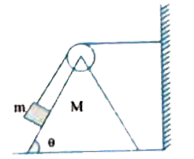
A block of mass m is arranged on the wedge as shown in figure . The wedge angle is θ. If the masses of pulley and thread and negligible and friction is absent , find the acceleration of the wedge
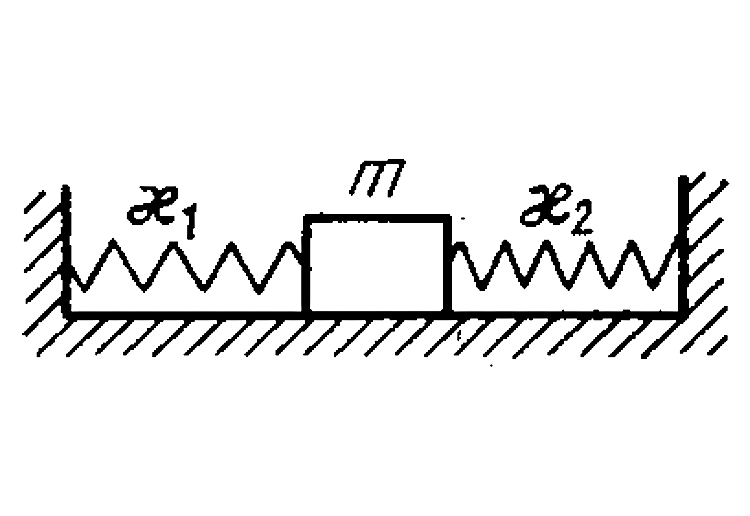
View SolutionDetermine the period of small longitudinal oscillations of a body with mass m in the system shown in figure. The stiffness values of the springs are x1 and x2. The friction and the masses of the springs are negligible.
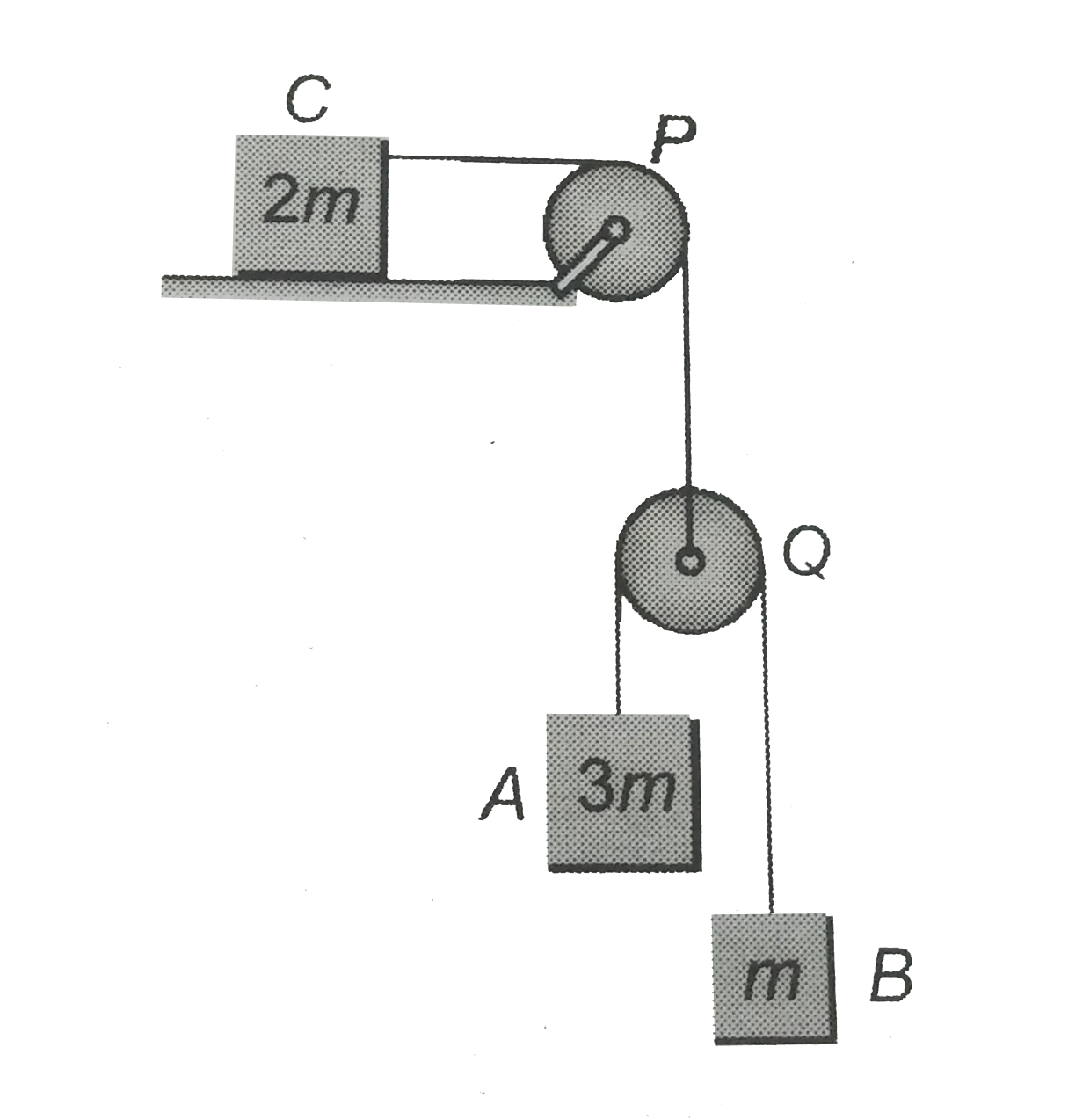
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View SolutionThe string, the spring and the pulley shown in figure are light. Find the time period of the mass m.

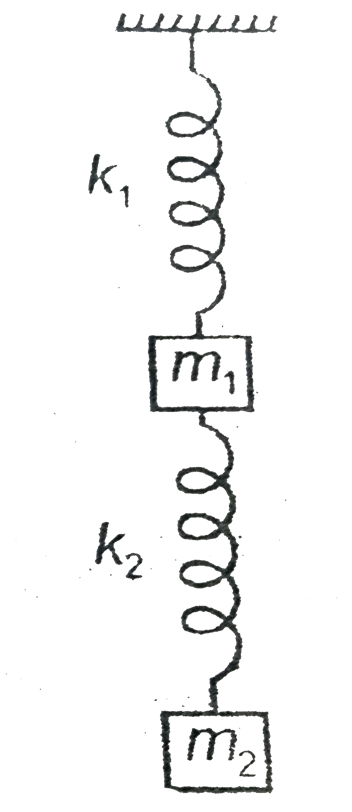
View SolutionFind the ratio of the extension in upper spring to lower spring
View Solution
Consider the situation as shown. Initially the spring is unstretched when the block of mass m is released from rest assuming the pulley frictionless and light the spring and string massless. Find the extension of sprinig when the block is in equilibrium also find the maximum extension of the spring.
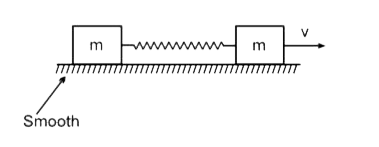
View SolutionTwo masses are connected by a spring as shown in the figure. One of the masses was given velocity v = 2 k, as shown in figure where 'k' is the spring constant. Then maximum extension in the spring will be
View Solution
