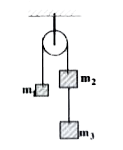
A massless string passes over a frictionless pulley and carries mass $m_{1}$ hanging at one end and mass $m_{2}$ connected by another massless string to mass $m_{3}$ at other end as shown in figure. Calculate the tension in string joining masses $m_{2} and m_{3}$ .

Text Solution

Verified by Experts

Let $T_{1}$ be the tension in the string joining $m_{1} and m_{2}$ , while $T_{2}$ the tension is string joining $m_{2} and m_{3}$ .
Let a be acceleration of masses. The resultant force on mass $m_{3}$ is $(m_{3} g - T)$ downward, therefore, we have
$m_{3} g - T_{2} = m_{3} a$ ......... (1)
Resultant force on mass $m_{2}$ is
$(m_{2} g + T_{2} - T_{1})$ downwards , therefore , we have
$m_{2} g + T_{2} - T_{1} = m_{2} a$ ...... (2)
Reusultant force on mass $m_{1}$ is $(T_{1} - m_{1} g)$ upward , therefore , we have
$T_{1} - m_{1} g = m_{1} a$ ........ (3)
Adding (1) , (2) and (3) , we get , $m_{3} g + m_{2} g - m_{1} g = (m_{3} + m_{2} + m_{1}) a$
$∴$ acceleration $a = \frac{(m_{2} + m_{3} - m_{1})}{m_{1} + m_{2} + m_{3}} g$
substituting this value of a in (1) , we get
$m_{3} g - T_{2} = m_{3} . \frac{(m_{2} + m_{3} - m_{1}) g}{m_{1} + m_{2} + m_{3}}$
This gives $T_{2} = m_{3} g - \frac{m_{3} (m_{2} + m_{3} - m_{1}) g}{m_{1} + m_{2} + m_{3}}$
$∴$ Requried Tension , $T_{2} = \frac{2 m_{1} m_{3} g}{m_{1} + m_{2} + m_{3}}$ .

Updated on:21/07/2023