In a series LCR circuit, the voltage across the resistance, capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
10V
10√2V
10√2V
20V
The correct Answer is:C
To solve the problem, we need to analyze the given series LCR circuit and determine the voltage across the inductance when the capacitance is short-circuited.
1. Understand the Initial Conditions:
- In the series LCR circuit, the voltage across the resistance (R), capacitance (C), and inductance (L) is given as 10 V each.
2. Identify the Impedance:
- The total voltage across the circuit can be expressed using the impedance of the circuit. In a series LCR circuit, the impedance (Z) is given by:
Z=√R2+(XL−XC)2
- Where XL is the inductive reactance and XC is the capacitive reactance.
3. Calculate the Equivalent Resistance:
- Since the voltage across each component is 10 V, we can express the current (I) in terms of the resistance:
V=I⋅R⟹I=10R
4. Short-Circuit the Capacitance:
- When the capacitance is short-circuited, the capacitive reactance XC becomes 0. Thus, the impedance of the circuit simplifies to:
Z=√R2+X2L
5. Recalculate the Current:
- The new current in the circuit can be calculated using the voltage across the resistance:
I=VZ=10√R2+X2L
6. Determine the Voltage Across the Inductance:
- The voltage across the inductance VL can be calculated as:
VL=I⋅XL
- Substituting the expression for I gives:
VL=⎛⎜
⎜⎝10√R2+X2L⎞⎟
⎟⎠⋅XL
7. Substituting Values:
- Since initially, the voltage across the inductance was 10 V, we can relate XL to the resistance R:
XL=R⟹VL=10⋅R√R2+R2=10R√2R2=10RR√2=10√2≈7.07V
8. Final Answer:
- The voltage across the inductance when the capacitance is short-circuited is:
VL=10√2 V
- In the series LCR circuit, the voltage across the resistance (R), capacitance (C), and inductance (L) is given as 10 V each.
- The total voltage across the circuit can be expressed using the impedance of the circuit. In a series LCR circuit, the impedance (Z) is given by:
Z=√R2+(XL−XC)2
- Where XL is the inductive reactance and XC is the capacitive reactance.
- Since the voltage across each component is 10 V, we can express the current (I) in terms of the resistance:
V=I⋅R⟹I=10R
- When the capacitance is short-circuited, the capacitive reactance XC becomes 0. Thus, the impedance of the circuit simplifies to:
Z=√R2+X2L
- The new current in the circuit can be calculated using the voltage across the resistance:
I=VZ=10√R2+X2L
- The voltage across the inductance VL can be calculated as:
VL=I⋅XL
- Substituting the expression for I gives:
VL=⎛⎜
⎜⎝10√R2+X2L⎞⎟
⎟⎠⋅XL
- Since initially, the voltage across the inductance was 10 V, we can relate XL to the resistance R:
XL=R⟹VL=10⋅R√R2+R2=10R√2R2=10RR√2=10√2≈7.07V
- The voltage across the inductance when the capacitance is short-circuited is:
VL=10√2 V
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 250videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
In a series L-C-R circuit the voltage across resistance , capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
View SolutionIn a series LCR the voltage across resistance, capacitance and inductance is 10V each. If the capacitance is shor t circulated, the voltage across the inducatance will be
View Solution
Knowledge Check
- Question 1 - Select One
In a series LCR circuit the voltage across an inductor, capacitor and resistor are 20 V, 20 V and 40 V respectively. The phase difference between the applied voltage and the current in the circuit is
A30∘B45∘C60∘D0∘
In the given circuit , the voltage across the base emitter junction is
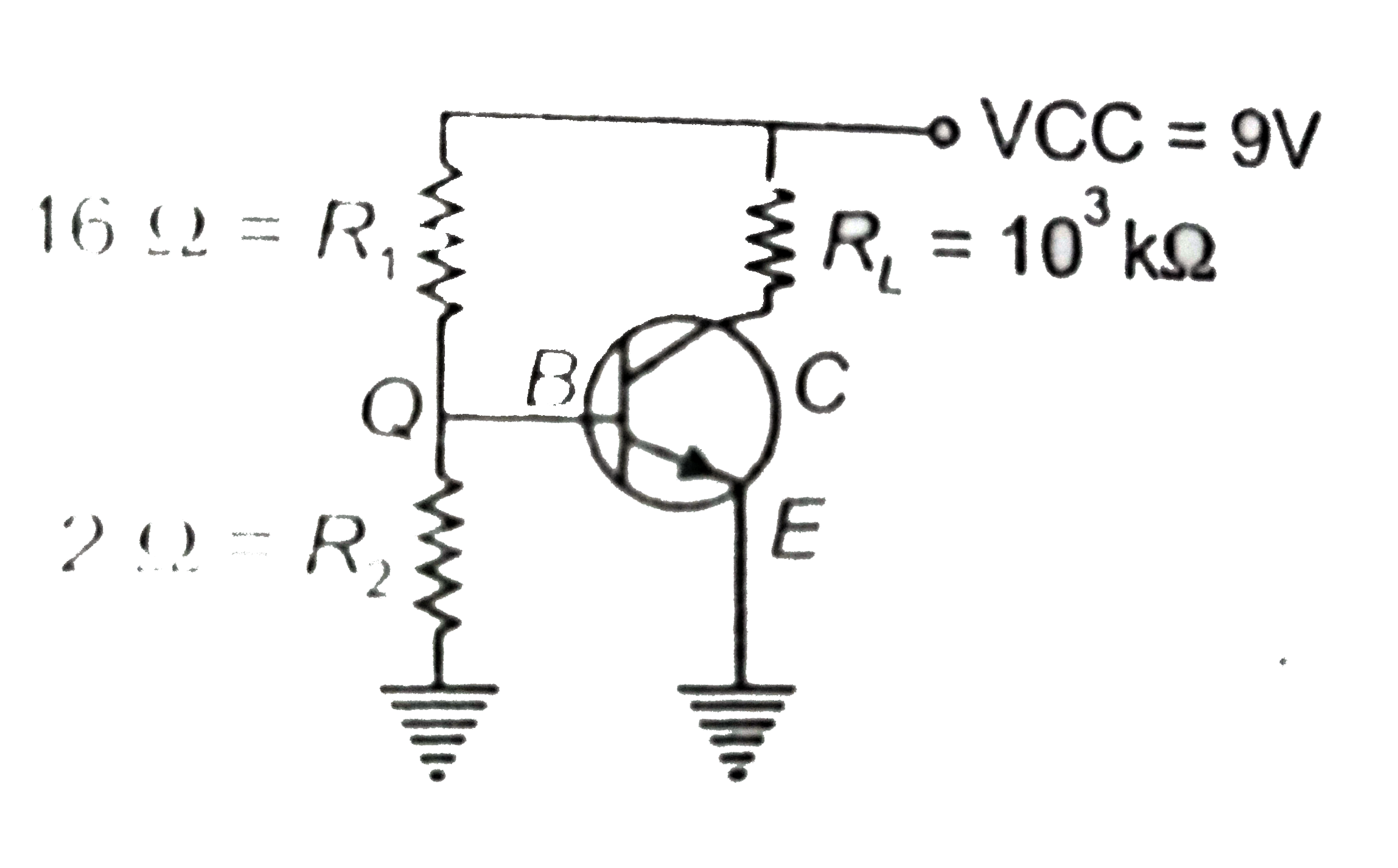 View Solution
View SolutionIn a series LCR circuit the rms voltage across the inductance , capacitance and resistance are respectively 4 V, 8 V and 5 V . The RMS voltage of the AC source in the circuit is
View SolutionIn series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View SolutionIn a series resonant circuit, the ac, voltage across resistance R, inductance L and capacitance are 5V, 10V and 10V, respectively. The ac. voltage applied to the circuit will be
View SolutionThe potential differences across the resistance, capacitance and inductance are 80V,40V and 100V respectively in an L−C−R circuit. The power factor of this circuit is
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View SolutionIn series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source
 View Solution
View Solution

