Natural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
4.9 cm
0.49 cm
9.4 cm
0.94 cm
The correct Answer is:A
To find the extension produced in the spring when a mass is hung from it, we can follow these steps:
1. Identify the Given Values:
- Natural length of the spring, L=60cm (not directly needed for extension calculation)
- Spring constant, k=4000N/m
- Mass hung from the spring, m=20kg
- Acceleration due to gravity, g=9.8m/s2
2. Calculate the Weight of the Mass:
The weight W of the mass can be calculated using the formula:
W=m⋅g
Substituting the values:
W=20kg⋅9.8m/s2=196N
3. Apply Hooke's Law:
According to Hooke's Law, the force exerted by the spring is proportional to the extension x:
F=k⋅x
At equilibrium, the weight of the mass equals the spring force:
W=k⋅x
Therefore, we can set up the equation:
mg=kx
4. Rearranging the Equation to Solve for Extension x:
Rearranging gives us:
x=mgk
5. Substituting the Known Values:
Now substituting the values we calculated:
x=196N4000N/m
6. Calculating the Extension:
Performing the division:
x=0.049m
7. Convert to Centimeters:
To convert meters to centimeters, multiply by 100:
x=0.049m×100=4.9cm
8. Conclusion:
The extension produced in the spring is 4.9cm.
Final Answer:
The extension produced in the spring is 4.9 cm.
- Natural length of the spring, L=60cm (not directly needed for extension calculation)
- Spring constant, k=4000N/m
- Mass hung from the spring, m=20kg
- Acceleration due to gravity, g=9.8m/s2
The weight W of the mass can be calculated using the formula:
W=m⋅g
Substituting the values:
W=20kg⋅9.8m/s2=196N
According to Hooke's Law, the force exerted by the spring is proportional to the extension x:
F=k⋅x
At equilibrium, the weight of the mass equals the spring force:
W=k⋅x
Therefore, we can set up the equation:
mg=kx
Rearranging gives us:
x=mgk
Now substituting the values we calculated:
x=196N4000N/m
Performing the division:
x=0.049m
To convert meters to centimeters, multiply by 100:
x=0.049m×100=4.9cm
The extension produced in the spring is 4.9cm.
The extension produced in the spring is 4.9 cm.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills8videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems9videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar6videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason10videos
PHYSICAL WORLD
Similar Questions
A block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g=10ms−2)
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionA spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)
View SolutionA spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)
View SolutionA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
View SolutionA mass hangs in equilibrium from a spring of constant K=2N/cmAnother mass of 3 kg is placed over M. Find the new amplitude of oscillation after wards (in m) (Takeg=10m/s−2)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural lengthView Solution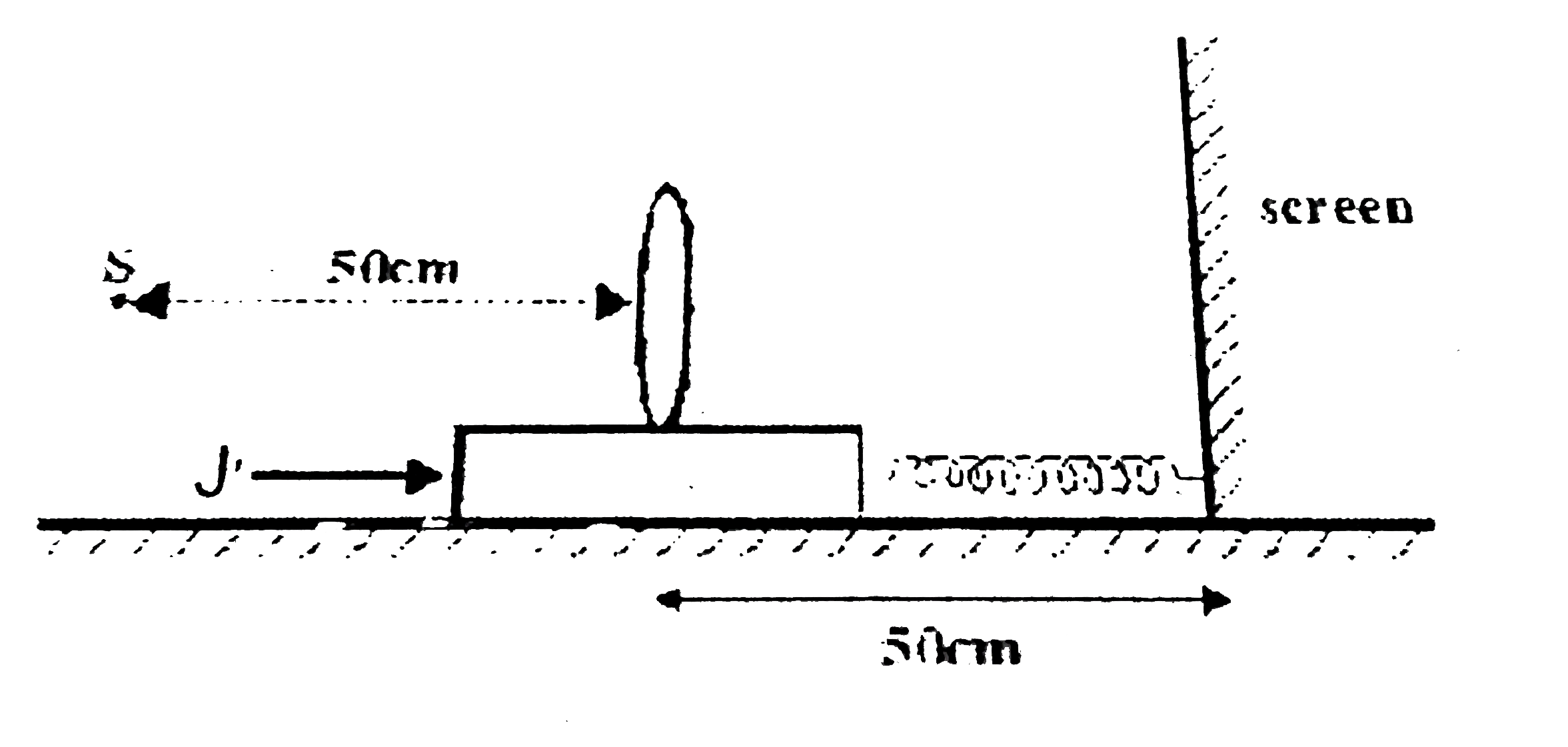
A point is located at a distance 100 cm from the screen. A lens of focal length 23 cm mounted on a movable frictionless stand is kept between the object and screen. The stand is attached to massless spring of natural length 50 cm and spring constant 800Nm as shown in the figure. Mass of the stand with lens is 2 kg. Initially spring is in its natural length. Now a sharp impulse J is given to the stand. Answer the following questions.
Q. Choose the correct options (s):View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA mass m = 8kg is attached to a spring as shown in figure and held in positioin so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
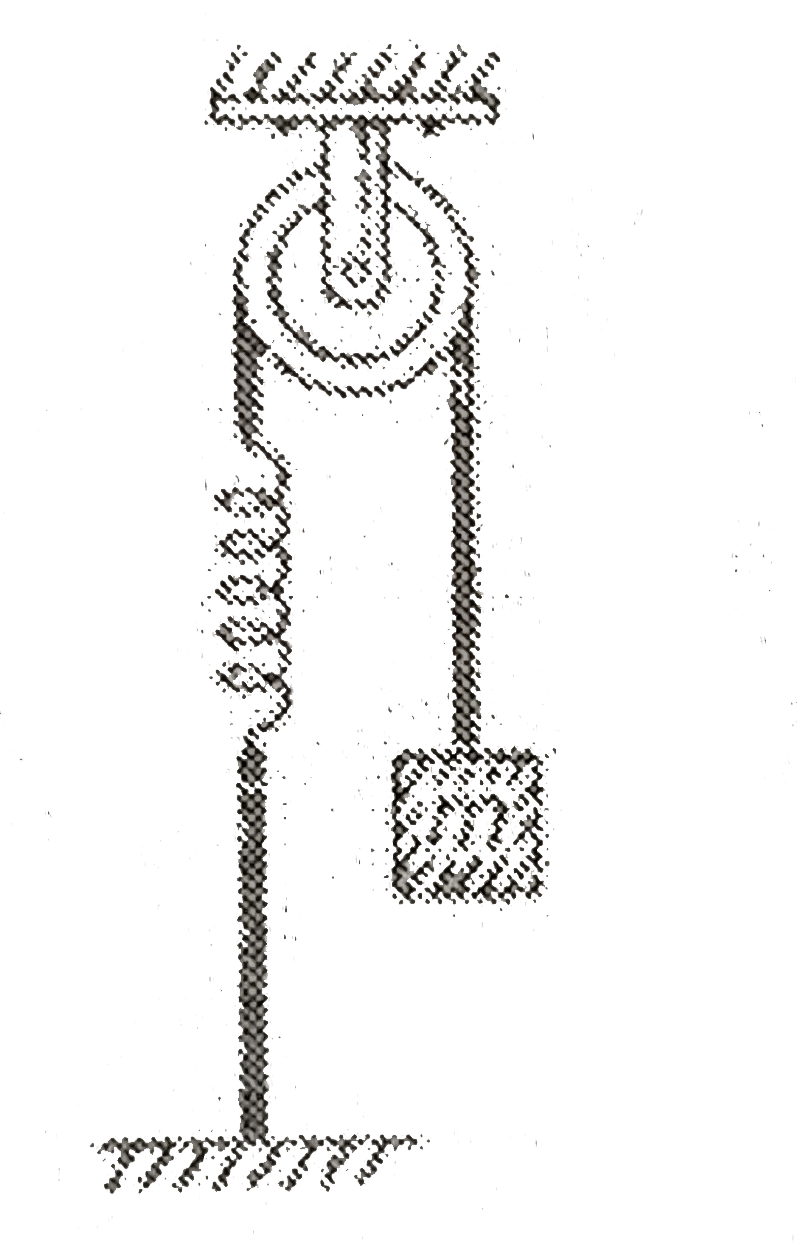 View Solution
View Solution

